《2025年练习部分九年级数学上册沪教版54制》

2. 如图,已知点D、E分别在△ABC的边BA、CA的延长线上,且DE//BC.
(1) 如果AD= 3,AB= 6,DE= 4,求BC的长.
(2) 如果$\frac{DE}{BC}= \frac{2}{5}$,CE= 14,求AE的长.

答案： 解：
(1)
∵DE//BC，
∴△ADE∽△ABC，


∴$\frac {DE}{BC}=\frac {AD}{AB}，$即$\frac {4}{BC}=\frac {3}{6}，$


∴BC=8.
(2)
∵DE//BC，

∴△ADE∽△ABC，


∴$\frac {DE}{BC}=\frac {AE}{AC}=\frac {2}{5}.$


∵CE=14，

∴$\frac {AE}{14-AE}=\frac {2}{5}，$

∴AE=4.

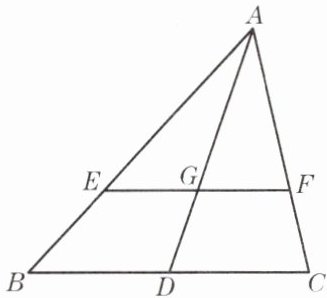
3. 如图,已知AD是△ABC的边BC上的中线,G是△ABC的重心,EF过点G且平行于BC,分别交AB、AC于点E、F. 求AF：FC和EF：BC的值.

答案： 解：
∵G是三角形的重心，且AD是BC边上的中线，
∴AG：GD=2：1，AG：AD=2：3.
∵EF//BC，
∴△AGF∽△ADC，△AEF∽△ABC，
∴AF：FC=AG：GD=2：1=2
EF：BC=AF：AC=AG：AD=2：$3=\frac {2}{3}$

4. 如图,花丛中一根灯杆AB上有一盏路灯A. 灯光下,小明在D点处的影长DE= 3米,沿BD方向走到点G,DG= 5米,这时小明的影长GH= 4米. 如果小明的身高为1.7米,求路灯A离地面的高度.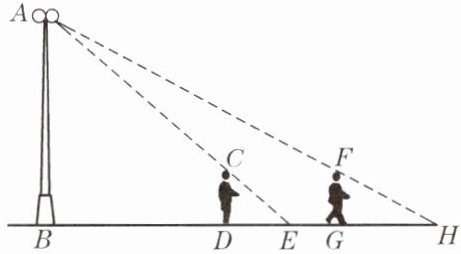

答案： 解：
∵CD//AB，
∴△EAB∽△ECD，
∴$\frac {CD}{AB}=\frac {DE}{BE}，$
即$\frac {1.7}{AB}=\frac {3}{3+BD}①，$
∵FG//AB，
∴△HFG∽△HAB，
∴$\frac {FG}{AB}=\frac {HG}{HB}，$
即$\frac {1.7}{AB}=\frac {4}{BD+5+4}②，$
由①②得$\frac {3}{3+BD}=\frac {4}{BD+5+4}，$解得BD=15，
∴$\frac {1.7}{AB}=\frac {3}{15+3}，$解得AB=10.2．
答：路灯A离地面的高度为10.2m．