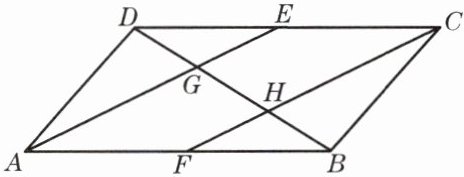
6. 如图,已知平行四边形ABCD中,点E、F分别是边DC、AB的中点,AE、CF与对角线BD分别交于点G、H,设$\overrightarrow{AF}= \overrightarrow{a}$,$\overrightarrow{AD}= \overrightarrow{b}$。
(1)试用$\overrightarrow{a}$、$\overrightarrow{b}分别表示向量\overrightarrow{GH}$、$\overrightarrow{GE}$。
(2)作出向量$\overrightarrow{DH}分别在\overrightarrow{a}$、$\overrightarrow{b}$方向上的分向量。
(1)试用$\overrightarrow{a}$、$\overrightarrow{b}分别表示向量\overrightarrow{GH}$、$\overrightarrow{GE}$。
(2)作出向量$\overrightarrow{DH}分别在\overrightarrow{a}$、$\overrightarrow{b}$方向上的分向量。

答案:
解:$(1)\because $四边形ABCD是平行四边形,
$ \therefore CD=AB,$CD//AB,
$ \because DE=CE,$AF=FB,
$ \therefore CE=AF,$CE//AF,
$ \therefore $四边形AECF是平行四边形,$\therefore AE//CF,$
$ \because EG∥CH,$DE=EC,
$ \therefore DG=GH,$同理可证BH=GH,$\therefore DG=GH=HB,$
$ \because \overrightarrow{AF}=\overrightarrow{a},$$\overrightarrow{AD}=\overrightarrow{b},$
$ \therefore \overrightarrow{DA}=-\overrightarrow{b},$$AB=2\overrightarrow{a},$
$ \therefore \overrightarrow{DB}=2\overrightarrow{a}-\overrightarrow{b},$
$ \therefore \overrightarrow{GH}=\overrightarrow{DG}=\frac {1}{3}\overrightarrow{BD}=\frac {2}{3}\overrightarrow{a}-\frac {1}{3}\overrightarrow{b},$
$ \because \overrightarrow{GE}=\overrightarrow{GD}+\overrightarrow{DE},$$\overrightarrow{GD}=\frac {1}{3}\overrightarrow{b}-\frac {2}{3}\overrightarrow{a},$$\overrightarrow{DE}=\overrightarrow{AF}=\overrightarrow{a},$
$ \therefore \overrightarrow{GE}=\frac {1}{3}\overrightarrow{b}+\frac {1}{3}\overrightarrow{a}.$
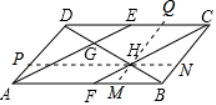
(2)如图所示,$\overrightarrow{DQ},$$\overrightarrow{DP}$即为所求.
解:$(1)\because $四边形ABCD是平行四边形,
$ \therefore CD=AB,$CD//AB,
$ \because DE=CE,$AF=FB,
$ \therefore CE=AF,$CE//AF,
$ \therefore $四边形AECF是平行四边形,$\therefore AE//CF,$
$ \because EG∥CH,$DE=EC,
$ \therefore DG=GH,$同理可证BH=GH,$\therefore DG=GH=HB,$
$ \because \overrightarrow{AF}=\overrightarrow{a},$$\overrightarrow{AD}=\overrightarrow{b},$
$ \therefore \overrightarrow{DA}=-\overrightarrow{b},$$AB=2\overrightarrow{a},$
$ \therefore \overrightarrow{DB}=2\overrightarrow{a}-\overrightarrow{b},$
$ \therefore \overrightarrow{GH}=\overrightarrow{DG}=\frac {1}{3}\overrightarrow{BD}=\frac {2}{3}\overrightarrow{a}-\frac {1}{3}\overrightarrow{b},$
$ \because \overrightarrow{GE}=\overrightarrow{GD}+\overrightarrow{DE},$$\overrightarrow{GD}=\frac {1}{3}\overrightarrow{b}-\frac {2}{3}\overrightarrow{a},$$\overrightarrow{DE}=\overrightarrow{AF}=\overrightarrow{a},$
$ \therefore \overrightarrow{GE}=\frac {1}{3}\overrightarrow{b}+\frac {1}{3}\overrightarrow{a}.$
(2)如图所示,$\overrightarrow{DQ},$$\overrightarrow{DP}$即为所求.

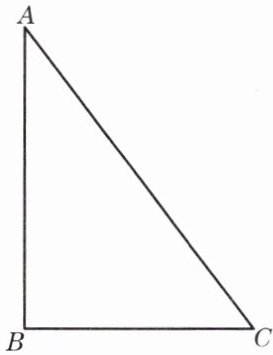
7. 如图,△ABC表示一块直角三角形空地,$\angle ABC= 90^\circ$,边AB= 80分米,BC= 60分米。现要在空地内划出一个正方形区域建造水池,这个正方形的四个顶点必须在△ABC的边上。请你在图中画出一个符合要求的正方形,并求这个正方形的面积。再想一想,怎样设计才能使划出的正方形区域的面积最大?

答案:
解:如图,设正方形BDEF的边长为x分米,则AD=(80-x)分米.
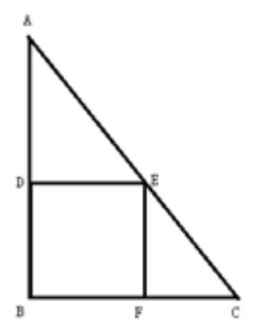
根据勾股定理得:$AC=\sqrt{{AB}^2{+BC}^2}=100$分米.
∵DE//BC,
∴△ADE∽△ABC,
∴$\frac {AD}{AB}=\frac {DE}{BC},$
∴$\frac {80-x}{80}=\frac {x}{60},$
∴$x=\frac {240}{7}$
这样设计正方形区域的面积是最大的
解:如图,设正方形BDEF的边长为x分米,则AD=(80-x)分米.

根据勾股定理得:$AC=\sqrt{{AB}^2{+BC}^2}=100$分米.
∵DE//BC,
∴△ADE∽△ABC,
∴$\frac {AD}{AB}=\frac {DE}{BC},$
∴$\frac {80-x}{80}=\frac {x}{60},$
∴$x=\frac {240}{7}$
这样设计正方形区域的面积是最大的
查看更多完整答案,请扫码查看


