2. 已知△ABC的三边长分别为20厘米、50厘米、60厘米,现要利用长度分别为30厘米和60厘米的细木条各一根,做一个与△ABC相似的三角形木架,要求以其中一根为一边,将另一根截成两段(允许有余料)作为另外两边,那么另外两边的长(单位:厘米)的所有可能情况是(
A.10,25;
B.10,36或12,36;
C.12,36;
D.10,25或12,36。
D
)A.10,25;
B.10,36或12,36;
C.12,36;
D.10,25或12,36。
答案:
D
3. 如图,5个同样大小的正方形拼成一个长方形,求$\angle ABC+\angle ADC+\angle ACB$的度数。
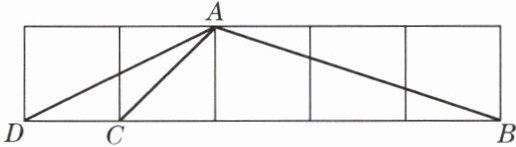

答案:
解:设每个小正方形的边长为1,
由勾股定理得:$AC=\sqrt {2},$$AD=\sqrt {5},$$AB=\sqrt {10},$
又
∵DC=1,BD=5,
∴$\frac {AD}{BD}=\frac {\sqrt{5}}{5},$$\frac {AC}{AB}=\frac {\sqrt{5}}{5},$
$ \frac {CD}{AD}=\frac {\sqrt{5}}{5}$
∴$\frac {AD}{BD}=\frac {AC}{AB}=\frac {CD}{AD},$
∴△ADC∽△BDA,
∴∠DAC=∠ABD,
∵∠ACB=45°,
∴∠ACB=∠DAC+∠ADB=45°,
∴∠ABC+∠ADC+∠ACB=90°.
由勾股定理得:$AC=\sqrt {2},$$AD=\sqrt {5},$$AB=\sqrt {10},$
又
∵DC=1,BD=5,
∴$\frac {AD}{BD}=\frac {\sqrt{5}}{5},$$\frac {AC}{AB}=\frac {\sqrt{5}}{5},$
$ \frac {CD}{AD}=\frac {\sqrt{5}}{5}$
∴$\frac {AD}{BD}=\frac {AC}{AB}=\frac {CD}{AD},$
∴△ADC∽△BDA,
∴∠DAC=∠ABD,
∵∠ACB=45°,
∴∠ACB=∠DAC+∠ADB=45°,
∴∠ABC+∠ADC+∠ACB=90°.
4. 如图,已知点P在等边三角形ABC的边BC的延长线上,$\angle PAQ= 120^\circ$,射线AQ与CB的延长线交于点Q。那么△ABQ与△PCA是否相似?为什么?
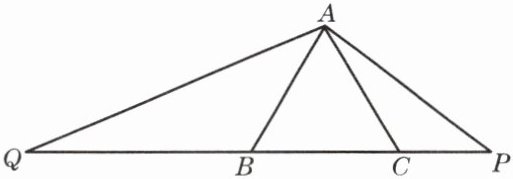

答案:
解:△ABQ与△PCA相似,理由如下:
∵△ABC为等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,
∴∠ABQ=∠ACP=180°-60°=120°.
∵∠PAQ=120°,
∴∠QAB+∠PAC=∠PAQ-∠BAC=60°.
∵∠ABC=∠Q+∠QAB=60°,
∴∠Q=∠PAC,
∴△ABQ与△PCA相似.
∵△ABC为等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,
∴∠ABQ=∠ACP=180°-60°=120°.
∵∠PAQ=120°,
∴∠QAB+∠PAC=∠PAQ-∠BAC=60°.
∵∠ABC=∠Q+∠QAB=60°,
∴∠Q=∠PAC,
∴△ABQ与△PCA相似.
5. 如图,已知梯形ABCD中,$AD// BC$,对角线AC与BD相交于点O,$S_{\triangle AOD}= 9$,$S_{\triangle BOC}= 16$。求$S_{梯形ABCD}$。
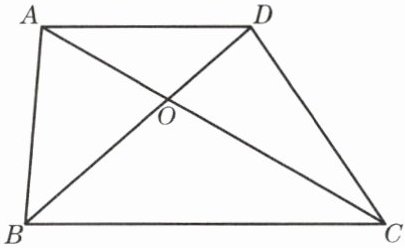

答案:
解:
∵AD//BC,
∴△AOD∽△COB,
∴$\frac {S_{△AOD}}{S_{△COB}}=\frac {9}{16},$
∴$\frac {OA}{OC}=\frac {3}{4},$
∵$\frac {S_{△AOD}}{S_{△DOC}}=\frac {OA}{OC}=\frac {3}{4},$
∴S_{△DOC}=12,
∴S_{△AOB}=S_{△DOC}=12,
∴梯形ABCD的面积=S_{△DOC}+S_{△AOB}+S_{△COB}+S_{△AOD}=9+12+12+16=49.
∵AD//BC,
∴△AOD∽△COB,
∴$\frac {S_{△AOD}}{S_{△COB}}=\frac {9}{16},$
∴$\frac {OA}{OC}=\frac {3}{4},$
∵$\frac {S_{△AOD}}{S_{△DOC}}=\frac {OA}{OC}=\frac {3}{4},$
∴S_{△DOC}=12,
∴S_{△AOB}=S_{△DOC}=12,
∴梯形ABCD的面积=S_{△DOC}+S_{△AOB}+S_{△COB}+S_{△AOD}=9+12+12+16=49.
查看更多完整答案,请扫码查看


