《2025年练习部分九年级数学上册沪教版54制》

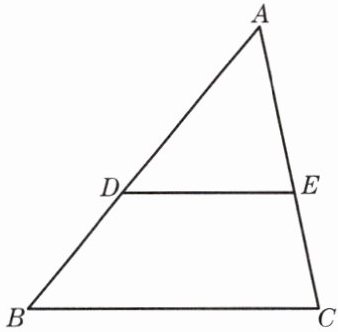
3. 已知点D、E分别在△ABC的边AB和AC上,DE//BC,△ABC的面积为S,BC= a,△ADE的面积为$S_1. $求DE的长(用字母S、$S_1、$a的代数式表示).

答案：
解：因为DE//BC
所以△ADE∽△ABC
所以$(\frac {DE}{BC})²=\frac {S_{△ADE}}{S_{△ABC}}$
所以$(\frac {DE}{a})²=\frac {S_1}{S}$
所以$\frac {DE}{a}=\sqrt{\frac {S_1}{S}}$
所以$DE=\frac {a\sqrt{SS_1}}{S}$

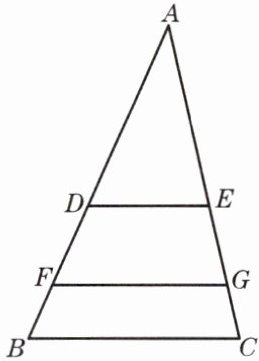
4. 如图,已知△ABC中,点D、F在边AB上,点E、G在边AC上,平行于BC的直线DE和FG将△ABC的面积分成相等的三部分,BC= 15厘米. 求DE、FG的长.

答案： 解：因为DE//BC
所以△ADE∽△ABC
所以$(\frac {DE}{BC})²=\frac {S_{△ADE}}{S_{△ABC}}=\frac {1}{3}$
所以$\frac {DE}{15}=\frac {1}{\sqrt{3}}$
所以$DE=5\sqrt{3}$厘米
因为FG//BC
所以△AFG∽△ABC
所以$(\frac {FG}{BC})²=\frac {S_{△AFG}}{S_{△ABC}}=\frac {2}{3}$
所以$\frac {FG}{15}=\frac {\sqrt{2}}{\sqrt{3}}$
所以$FG=5\sqrt{6}\ \mathrm {cm}.$

1. 把同一个三角形地块按不同的比例尺画成甲乙两个图.设甲图的比例尺为 $1:200$,乙图的比例尺为 $1:1000$,求甲图与乙图的相似比和面积比.

答案： 解：甲图与乙图的相似比$=\frac {\frac {1}{200}}{\frac {1}{1000}}=5$：1
面积的比为$5^2=25$：1