《2025年练习部分九年级数学上册沪教版54制》

1. 如图,已知△PQR中,∠R= 90°.填空：


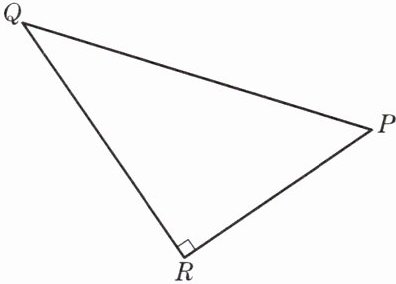
(1) $\frac{QR}{PR}=$tanP=cotQ；(用含三角比的式子表示)
(2) $\frac{PR}{PQ}=$sinQ=cosP.(用含三角比的式子表示)

答案： tanP
cotQ
sinQ
cosP

2. 如图,已知△ABC中,∠C= 90°,∠B= α,AC= m.

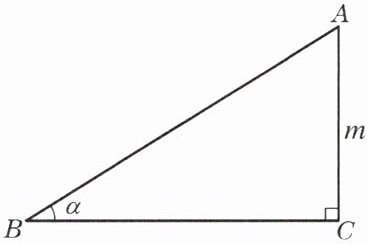
(1) 用含α和m 的式子表示 BC.(用两种方法)
(2) 用含α和m 的式子表示 AB.

答案： 解：
(1)方法一：
∵△ABC中，∠C=90°，∠B=α，AC=m，
∴$tanα=\frac {m}{BC}，$
∴$BC=\frac {m}{tanα}.$
方法二：
∵△ABC中，∠C=90°，∠B=α，AC=m，
∴∠A=90°-α，$tan∠A=\frac {BC}{AC}，$
∴$tan(90°-α)=\frac {BC}{m}，$
∴BC=mtan(90°-α).
解：
(2)
∵△ABC中，∠C=90°，∠B=α，AC=m，
∴$sinα=\frac {m}{AB}，$
∴$AB=\frac {m}{sinα}.$

3. 求下列各式的值(结果保留根号)：
(1) $\cot^{2}30^{\circ}-\frac{\cos45^{\circ}}{\tan45^{\circ}+\sin45^{\circ}}$.
(2) $\sqrt{\cos^{2}30^{\circ}-\sin^{2}30^{\circ}}+\frac{\sin60^{\circ}}{\tan60^{\circ}}$.

答案： 解：$(1)cot^{2}30°-\frac {cos{45}°}{tan{45}°+sin{45}°}$
$ =(\sqrt{3})^2-\frac {\frac {\sqrt{2}}{2}}{1+\frac {\sqrt{2}}{2}}$
$ =3-(\sqrt{2}-1)$
$ =4-\sqrt{2}.$
$ (2)\sqrt{cos^230°-sin^230°}+\frac {sin{60}°}{tan{60}°}$
$ =\sqrt{(\frac {\sqrt{3}}{2}{)}^2-(\frac {1}{2}{)}^2}+\frac {\frac {\sqrt{3}}{2}}{\sqrt{3}}$
$ =\frac {\sqrt{2}}{2}+\frac {1}{2}$
$ =\frac {\sqrt{2}+1}{2}.$