《2025年练习部分九年级数学上册沪教版54制》

14. 如图,已知向量$\vec{a}$、$\vec{b}和\vec{p}$,求作：(1)向量$-3\vec{a}+\frac{1}{2}\vec{b}$.(2)向量$\vec{p}分别在\vec{a}$、$\vec{b}$方向上的分向量.

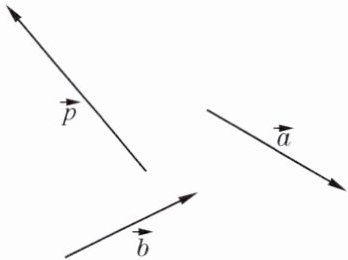
答案：
解：
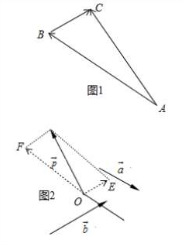
(1)向量$\overrightarrow{AC}=-3\overrightarrow{a}+\frac {1}{2}\overrightarrow{b}，$如图1中所示.
(2)向量$\overrightarrow{p}$分别在$\overrightarrow{a}、$$\overrightarrow{b}$方向上的分向量$\overrightarrow{OF}、$$\overrightarrow{OE}$如图所示.

15. 计算：(1)$-\frac{2}{3}(2\vec{a}+3\vec{b})-\frac{1}{3}(-\vec{b}-\frac{1}{2}\vec{a})$.(2)$2(-2\vec{a}+\vec{b}-3\vec{c})+(\vec{a}-2\vec{b}-3\vec{c})$.

答案： 解：原式$=-\frac {4}{3}\overrightarrow{a}-2\overrightarrow{b}+\frac {1}{3}\overrightarrow{b}+\frac {1}{6}\overrightarrow{a}$
$ =-\frac {7}{6}\overrightarrow{a}-\frac {5}{3}\overrightarrow{b}$
解：原式$=-4\overrightarrow{a}+2\overrightarrow{b}-6\overrightarrow{c}+\overrightarrow{a}-2\overrightarrow{b}-3\overrightarrow{c}$
$ =-3\overrightarrow{a}-9\overrightarrow{c}$

1. 如图,已知点D、E分别在△ABC的边AB、AC上。
(1)如果$DE// BC$,且$S_{\triangle ADE}= 4$,$S_{\triangle BCE}= 24$,求$S_{\triangle BDE}$。
(2)如果$S_{\triangle ADE}= S_1$,$S_{\triangle BDE}= S_2$,那么当$S_{\triangle BCE}与S_1$、$S_2$满足什么等量关系时,$DE与BC$一定平行？

答案： 解：
(1)设 S_{ △BDE}=x，
∵ DE//BC
∴ △ADE∽△ABC
∴$ \frac { S_{ △ADE}}{ S_{ △ABC}}= (\frac { DE}{ BC})^{ 2}$
∵ △BDE与△BCE是等高三角形
∴$ \frac { S_{ △BDE}}{ S_{ △BCE}}=\frac { DE}{ BC}$
∴$ \frac { S_{ △ADE}}{ S_{ △ABC}}= (\frac { S_{ △BDE}}{ S_{ △BCE}})^{ 2}$
∵$ S_{ △ADE}=4\ \mathrm {S}_{ △BCE}=24$
∴$ \frac { 4}{ 28+x}= (\frac { x}{ 24})^{ 2}$
∴ x=8即 S_{ △BDE}=8
(2)假设DE//BC， S_{ △BCE}= S_{ 3}，
结合第一问可知$ \frac { S_{ △BDE}}{ S_{ △BCE}}= \frac { S_{ 2}}{ S_{ 3}}=\frac { DE}{ BC}$
∵ DE//BC
∴$ \frac { DE}{ BC}=\frac { AD}{ AB}$
∵ △ADE与△ABE等高
∴$ \frac { S_{ △ADE}}{ S_{ △ABE}}=\frac { AD}{ AB}$
即$ \frac { S_{ 1}}{ S_{ 1}+ S_{ 2}}=\frac { AD}{ AB}$
∴$ \frac { S_{ 1}}{ S_{ 1}+ S_{ 2}}=\frac { S_{ 2}}{ S_{ 3}}$
∴$ S_{ 3}=\frac { S_{ 2}× ( S_{ 1}+ S_{ 2})}{ S_{ 1}}$
因此，当$ S_{ △BCE}=\frac { S_{ 2}× ( S_{ 1}+ S_{ 2})}{ S_{ 1}}$时，DE//BC