《2025年练习部分九年级数学上册沪教版54制》

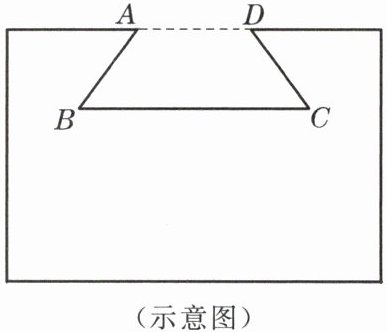
1. 如图,燕尾槽的横断面是等腰梯形ABCD,其中燕尾角∠B= 55°,外口宽AD= 180毫米,燕尾槽深度是70毫米,求它的里口宽BC(精确到1毫米).

答案：

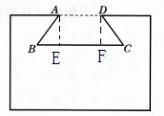
解：过点A作AE⊥CB于E，过点D作DF⊥CB于F，
于是可知，∠B=∠C=55°，$AD=180\ \mathrm {mm}，$$AE=DF=70\ \mathrm {mm}. $
∵AE⊥CB，DF⊥CB，AD//BC，$AD=180\ \mathrm {mm}，$
∴$EF=AD=180\ \mathrm {mm}.$
在Rt△ABE中，∠ABE=55°，$AE=70\ \mathrm {mm}，$
∴∠BAE=90°-55°=35°，
∴$BE=AEtan∠BAE=70×tan{35}°≈49.0(\ \mathrm {mm}).$
同理可得$CF≈49.0(\ \mathrm {mm}).$
∴$BC=BE+EF+CF≈49.0+180+49.0≈278(\ \mathrm {mm}).$
答：它的里口宽BC约为$278\ \mathrm {mm}.$

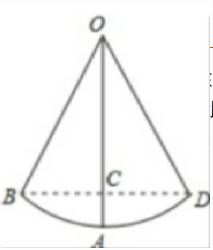
2. 一个杂技演员荡秋千,秋千绳子的长度为3.2米,当秋千向两边摆动的摆角恰好为60°时(摆动时两边的最高点与地面的距离相同),求摆动过程中最高点与最低点的高度差(精确到0.1米).

答案：
解:因为OA=OB=OD=3.2m，∠BOD= 60°
所以∠BOC= 30°
因为OA⊥BD于点C
所以$COS∠BOC=\frac{OC}{OB}$
所以OC=OB×cos{30}°
所以$CA=OA-OC=3.2-3.2×\ \mathrm {cos}30°≈0.4m$
即摆动过程中最高点与最低点的高度差0.4m。

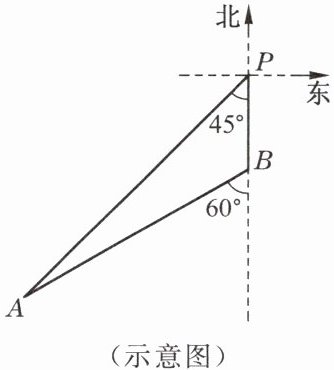
3. 如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P沿正南方向以每小时12海里的速度航行,1小时30分后到达B处,在B处测得小岛A在它的南偏西60°的方向上.小岛A离港口P有多少海里(精确到0.1海里)?

答案：
解：如图，作AE⊥PB于点E，

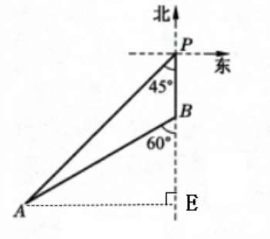
由题意得PB=12×1.5=18(海里).
设PE=x海里，
∵∠APE=45°，
∴PE=AE=x，
∴$BE=\frac {AE}{tan{60}°}=\frac {\sqrt{3}}{3}x，$
由题意得$PB=PE-BE=x-\frac {\sqrt{3}}{3}x=18，$
解得$x=27+9\sqrt{3}，$
∴$AP=\sqrt{2}PE=27\sqrt{2}+9\sqrt{6}≈60.2，$
故小岛A离港口P约有60.2海里.