搜索
6. 如图,
已知正方形$ABCD$中,$AB= 4$,点$E在边BC$上($E与B$、$C$不重合),点$F在边CD$上,$AE= AF$.设$\triangle AEF的面积为y$,$EC的长为x$,求$y关于x$的函数解析式及函数的定义域.
已知正方形$ABCD$中,$AB= 4$,点$E在边BC$上($E与B$、$C$不重合),点$F在边CD$上,$AE= AF$.设$\triangle AEF的面积为y$,$EC的长为x$,求$y关于x$的函数解析式及函数的定义域.
答案：
解：
∵四边形ABCD是正方形，
∴AB=AD，∠B=∠D=∠C=90°.
又
∵AE=AF，
∴△ABE≌△ADF，
∴EB=DF，
∴EC=FC=x，
∴BE=DF=4-x，
∴$S_{△AEF}=S_{正方形ABCD}-2S_{△ABE}-S_{△ECF}=4^2-2×\frac {1}{2}×4×(4-x)-\frac {1}{2}x^2=-\frac {1}{2}x^2+4x，$
故y与x之间的函数关系式为$y=-\frac {1}{2}x^2+4x，$函数的定义域为：0＜x≤4.
∵四边形ABCD是正方形，
∴AB=AD，∠B=∠D=∠C=90°.
又
∵AE=AF，
∴△ABE≌△ADF，
∴EB=DF，
∴EC=FC=x，
∴BE=DF=4-x，
∴$S_{△AEF}=S_{正方形ABCD}-2S_{△ABE}-S_{△ECF}=4^2-2×\frac {1}{2}×4×(4-x)-\frac {1}{2}x^2=-\frac {1}{2}x^2+4x，$
故y与x之间的函数关系式为$y=-\frac {1}{2}x^2+4x，$函数的定义域为：0＜x≤4.
1. 二次函数$ y= -3x^{2} $的图像的对称轴是
y轴
,顶点坐标是(0,0)
,开口方向向下
.
答案：
y轴
(0,0)
向下
(0,0)
向下
2. 在同一直角坐标系中,画出函数$ y= 2x^{2} 和 y= -2x^{2} $的图像.
答案：
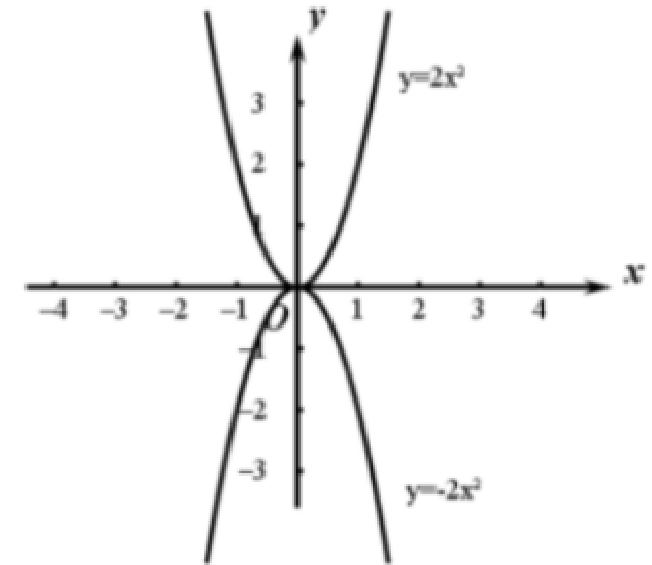
3. (1)如果抛物线$ y= ax^{2} $的开口向下,那么常数a的取值范围是
(2)抛物线$ y= -5x^{2} $有最
a＜0
.(2)抛物线$ y= -5x^{2} $有最
高
点(填“高”“低”).
答案：
a＜0
高
高
4. 已知二次函数$ y= ax^{2} 的图像经过点 A(-1,-\frac{1}{4}) $,求a的值,并写出这个函数的解析式.
答案：
解：将点A(-1，$-\frac {1}{4})$代入二次函数$y=ax^2$中，可得
$ -\frac {1}{4}=a×(-1)^2，$
解得，$a=-\frac {1}{4}.$
∴二次函数的解析式为$y=-\frac {1}{4}x^2.$
$ -\frac {1}{4}=a×(-1)^2，$
解得，$a=-\frac {1}{4}.$
∴二次函数的解析式为$y=-\frac {1}{4}x^2.$
查看更多完整答案，请扫码查看
