1. 已知点 P 在线段 AB 上,且 $AP:PB= 2:5$,那么 $AB:PB=$
7:5
,$AP:AB=$2:7
.
答案:
7:5
2:7
2:7
2. 求等边三角形的高与边长的比值.
答案:
解:设等边三角形的边长为a,则三角形的高为$\sqrt{{a}^2-(\frac {1}{2}a{)}^2}=\frac {\sqrt{3}}{2}a,$
则等边三角形的高与边长的比为$\frac {\sqrt{3}}{2}a$:$a=\sqrt{3}$:2,比值为$\frac {\sqrt{3}}{2}.$
则等边三角形的高与边长的比为$\frac {\sqrt{3}}{2}a$:$a=\sqrt{3}$:2,比值为$\frac {\sqrt{3}}{2}.$
3. 已知$\triangle ABC和\triangle A'B'C'$中,$\frac{AB}{A'B'}= \frac{BC}{B'C'}= \frac{CA}{C'A'}= \frac{3}{5}$,且$A'B'+B'C'+C'A'= 30$厘米,求$\triangle ABC$的周长.
答案:
解:
∵$\frac {AB}{A′B′}=\frac {BC}{B′C′}=\frac {CA}{C′A′}=\frac {3}{5},$
∴△ABC∽△A′B′C′,
∴△ABC的周长:△A′B′C′的周长=3:5.
∵$A′B′+B′C′+C′A′=30\ \mathrm {cm},$
∴△ABC的周长$=18\ \mathrm {cm}.$
∵$\frac {AB}{A′B′}=\frac {BC}{B′C′}=\frac {CA}{C′A′}=\frac {3}{5},$
∴△ABC∽△A′B′C′,
∴△ABC的周长:△A′B′C′的周长=3:5.
∵$A′B′+B′C′+C′A′=30\ \mathrm {cm},$
∴△ABC的周长$=18\ \mathrm {cm}.$
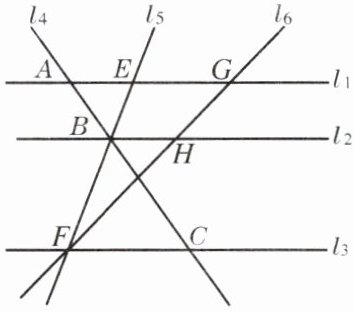
4. 如图,已知,直线$l_1$、$l_2$、$l_3依次截直线l_4$于点 A、B、C,截直线$l_5$于点 E、B、F,截直线$l_6$于点 G、H、F,且$l_1// l_2// l_3$,$BE= 2$,$BF= 4$,$AB= 2.5$,$FG= 9$.求 BC、FH、GH 的长.

答案:
解:
∵l_{1}//l_{2}//l_{3},
∴$\frac {AB}{BC}=\frac {BE}{BF}=\frac {GH}{FH},$
∴$\frac {2.5}{BC}=\frac {2}{4},$
∴BC=5,
∵FG=9,$\frac {GH}{FH}=\frac {1}{2},$
∴GH=3,FH=6.
∵l_{1}//l_{2}//l_{3},
∴$\frac {AB}{BC}=\frac {BE}{BF}=\frac {GH}{FH},$
∴$\frac {2.5}{BC}=\frac {2}{4},$
∴BC=5,
∵FG=9,$\frac {GH}{FH}=\frac {1}{2},$
∴GH=3,FH=6.
查看更多完整答案,请扫码查看


