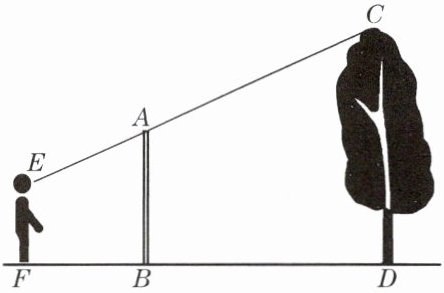
5. 如图,竖立在点 B 处的标杆$AB= 2.5$米,某观察者站立在点 F 处,从点 E 处看到杆顶 A、树顶 C 在一直线上(点 F、B、D 也在一直线上).已知$BD= 4.4$米,$FB= 2.2$米,人的眼睛离地面的距离$EF= 1.5$米,求树高.

答案:
由已知得EF⊥FD,AB⊥FD,CD⊥FD,
则四边形EFDH、四边形EFGB和四边形GBDH都是矩形,
∴EF=GB=DH=1.5米,EG=FB=2.2米,GH=BD=4.4米,
∴AG=AB-GB=2.5-1.5=1米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴$\frac {AG}{CH}=\frac {FG}{EH},$
∵EH=EG+GH=6.6米,
∴$CH=\frac {AG×EH}{EG}=3,$
∴CD=CH+HD=3+1.5=4.5米,
答:树高为4.5米.

由已知得EF⊥FD,AB⊥FD,CD⊥FD,
则四边形EFDH、四边形EFGB和四边形GBDH都是矩形,
∴EF=GB=DH=1.5米,EG=FB=2.2米,GH=BD=4.4米,
∴AG=AB-GB=2.5-1.5=1米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴$\frac {AG}{CH}=\frac {FG}{EH},$
∵EH=EG+GH=6.6米,
∴$CH=\frac {AG×EH}{EG}=3,$
∴CD=CH+HD=3+1.5=4.5米,
答:树高为4.5米.

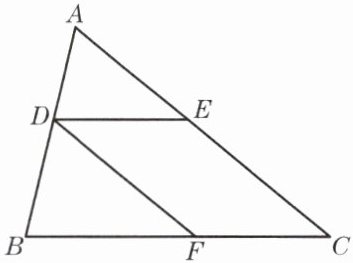
6. 如图,已知点 D、E、F 分别在$\triangle ABC$的边 AB、AC、BC 上,$DE// BC$、$DF// AC$,$AE= 6$,$CE= 8$.求$BF:FC$的值.

答案:
解:
∵DE//BC,
∴AD:BD=AE:EC=6:8=3:4,
∵DF//AC,
∴BF:FC=BD:DA=4:3.
∵DE//BC,
∴AD:BD=AE:EC=6:8=3:4,
∵DF//AC,
∴BF:FC=BD:DA=4:3.
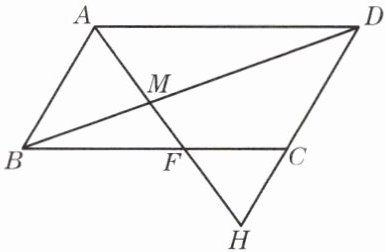
7. 已知:如图,M 是平行四边形 ABCD 的对角线 BD 上的一点,射线 AM 与 BC 交于点 F,与 DC 的延长线交于点 H.求证:$AM^2= MF\cdot MH$.

答案:
证明:因为四边形ABCD是平行四边形
所以AD//BC.AB//CD
所以△ADM∽△FBM,△DMH∽△BMA
所以$\frac {DM}{BM}=\frac {AM}{FM},$$\frac {DM}{BM}=\frac {HM}{AM}$
所以$\frac {AM}{FM}=\frac {HM}{AM}$
所以AM²=MF×MH
所以AD//BC.AB//CD
所以△ADM∽△FBM,△DMH∽△BMA
所以$\frac {DM}{BM}=\frac {AM}{FM},$$\frac {DM}{BM}=\frac {HM}{AM}$
所以$\frac {AM}{FM}=\frac {HM}{AM}$
所以AM²=MF×MH
查看更多完整答案,请扫码查看


