《2025年练习部分九年级数学上册沪教版54制》

1. 填空：
(1)已知非零向量$\vec{a}$,向量$\vec{b}= -5\vec{a}$,那么向量$\vec{a}与\vec{b}$的方向是相反,它们的关系是平行.
(2)已知$\vec{a}$、$\vec{b}$是两个不平行的向量,$\vec{c}= -\vec{a}+5\vec{b}$,那么向量$\vec{c}在\vec{a}$、$\vec{b}$方向上的分向量分别是$-\overrightarrow{a}$和$5\overrightarrow{b}$.

答案： 相反
平行
$-\overrightarrow{a}$和$5\overrightarrow{b}$

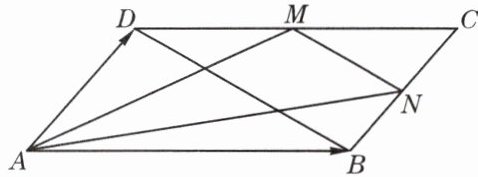
2. 如图,已知平行四边形$ABCD$中,点$M、N分别是边DC、BC$的中点.设$\overrightarrow{AB}= \vec{a},\overrightarrow{AD}= \vec{b}$,求向量$\overrightarrow{MN}、\overrightarrow{BD}分别在\vec{a}、\vec{b}$方向上的分向量.

答案： 解：
∵四边形ABCD是平行四边形，
∴AB//DC，AD//BC，AB=DC，AD=BC.
∵$\overrightarrow{AB}=\overrightarrow{a}，$$\overrightarrow{AD}=\overrightarrow{b}，$
∴$\overrightarrow{DC}=\overrightarrow{a}，$$\overrightarrow{BC}=\overrightarrow{b}.$
∵点M、N分别为DC、BC的中点，
∴DM=CM，BN=CN，
∴MN∥BD，$MN=\frac {1}{2}BD.$
∴$\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{a}+\overrightarrow{b}，$
∴$\overrightarrow{MC}=\frac {1}{2}\overrightarrow{a}，$$\overrightarrow{NC}=\frac {1}{2}\overrightarrow{b}，$
∴$\overrightarrow{MN}=\overrightarrow{MC}-\overrightarrow{NC}=\frac {1}{2}\overrightarrow{a}−\frac {1}{2}\overrightarrow{b}．$

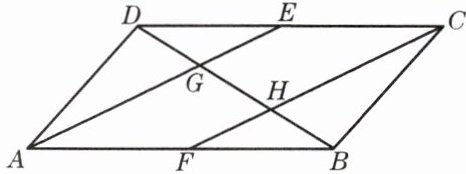
3. 如图,已知平行四边形$ABCD$中,$E、F分别是边DC、AB$的中点,$AE、CF分别与对角线BD相交于点G、H$,设$\overrightarrow{AB}= \vec{a},\overrightarrow{AD}= \vec{b}$,分别求向量$\overrightarrow{GE}、\overrightarrow{CH}关于\vec{a}、\vec{b}$的分解式.

答案： 解：
∵点E是边CD的中点，
四边形ABCD是平行四边形，
∴CD//AB，$DE=\frac {1}{2}CD=\frac {1}{2}AB，$
∴△ABG∽△EDG，
∴$\frac {EG}{AG}=\frac {DE}{AB}=\frac {1}{2}，$
∵$\overrightarrow{AB}=\overrightarrow{a}，$
∴$\overrightarrow{DE}=\frac {1}{2}\overrightarrow{a}，$
由向量三角形法则得
$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=\frac {1}{2}\overrightarrow{a}+\overrightarrow{b}，$
∴$\overrightarrow{GE}=\frac {1}{1+2}\overrightarrow{AE}=\frac {1}{6}\overrightarrow{a}+\frac {1}{3}\overrightarrow{b}.$
同理可得$\frac {CH}{FH}=2，$
∵$\overrightarrow{AB}=\overrightarrow{a}，$$\overrightarrow{AD}=\overrightarrow{b}，$
∴$\overrightarrow{CD}=-\overrightarrow{a}，$$\overrightarrow{CB}=-\overrightarrow{b}，$
∴$\overrightarrow{BF}=-\frac {1}{2}\overrightarrow{a}，$
由向量三角形法则得
$\overrightarrow{CF}=\overrightarrow{BF}+\overrightarrow{CB}=-\frac {1}{2}\overrightarrow{a}-\overrightarrow{b}，$
∴$\overrightarrow{CH}=\frac {1}{1+2}\overrightarrow{CF}$
$=\frac {2}{3}(-\frac {1}{2}\overrightarrow{a}-\overrightarrow{b})$
$=-\frac {1}{3}\overrightarrow{a}-\frac {2}{3}\overrightarrow{b}. $

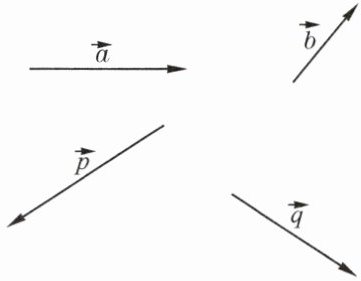
4. 如图,已知向量$\vec{a}、\vec{b}和\vec{p}、\vec{q}$,求作：
(1)向量$\vec{p}分别在\vec{a}、\vec{b}$方向上的分向量.
(2)向量$\vec{q}分别在\vec{a}、\vec{b}$方向上的分向量.

答案：
解：$(1)\overrightarrow{p}$在$\overrightarrow{a}，$$\overrightarrow{b}$方向上的分向量是$\overrightarrow{OD}，$$\overrightarrow{OE}.$
$ (2)\overrightarrow{q}$在$\overrightarrow{a}，$$\overrightarrow{b}$方向上的分向量为$\overrightarrow{OG}，$$\overrightarrow{OF}.$