7. 如图,已知△ABC中,∠ACB= 90°,CD⊥AB,垂足为D,CD= 4,$\cos A= \frac{3}{5}$.求:
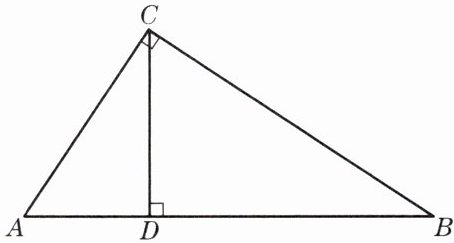
(1) AC的长.
(2) $\tan B$.

(1) AC的长.
(2) $\tan B$.
答案:
解:
(1)在Rt△ACD中,
$cosA=\frac {AD}{AC}=\frac {3}{5},$
设AD=3k,则AC=5k,
由勾股定理得,4k=4,
∴k=1,
∴AC=5.
(2)
∵∠ACB=90°,
∴∠A+∠B=90°.
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∴$tanB=tan∠ACD=\frac {AD}{CD}=\frac {3}{4}.$
(1)在Rt△ACD中,
$cosA=\frac {AD}{AC}=\frac {3}{5},$
设AD=3k,则AC=5k,
由勾股定理得,4k=4,
∴k=1,
∴AC=5.
(2)
∵∠ACB=90°,
∴∠A+∠B=90°.
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∴$tanB=tan∠ACD=\frac {AD}{CD}=\frac {3}{4}.$
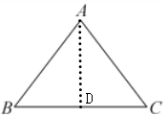
8. 已知△ABC中,AB= AC,BC= 10,$S_{\triangle ABC}= 60$.求:
(1) AB的长.
(2) ∠A(精确到 1′).
(1) AB的长.
(2) ∠A(精确到 1′).
答案:
解:依题意画出图形,作AD⊥BC交BC于D
∵S_{△ABC}=60,
∴$\frac {1}{2}×10×AD=60,$
解得AD=12.
∵AB=AC,BC=10,
∴$BD=\frac {1}{2}BC=5,$
∴AB=13.
(2)在Rt△ABD中,$sin∠BAD=\frac {BD}{AB}=\frac {5}{13}≈0.3864,$
∴∠BAD≈22.73°,
∴∠BAC=2∠BAD=45°26′.
解:依题意画出图形,作AD⊥BC交BC于D
∵S_{△ABC}=60,
∴$\frac {1}{2}×10×AD=60,$
解得AD=12.
∵AB=AC,BC=10,
∴$BD=\frac {1}{2}BC=5,$
∴AB=13.
(2)在Rt△ABD中,$sin∠BAD=\frac {BD}{AB}=\frac {5}{13}≈0.3864,$
∴∠BAD≈22.73°,
∴∠BAC=2∠BAD=45°26′.

9. 如图,小山的顶部是一块平地,在这块平地上有一高压输电线的铁架.小山斜坡 BD的坡度$i= 1:\sqrt{3}$,坡长为 50 米.在山坡的坡底 B 处测得铁架顶端 A 的仰角为 45°,在山坡的坡顶 D 处测得铁架顶端 A 的仰角为 60°.求铁架的高度 AE(精确到 0.1 米).
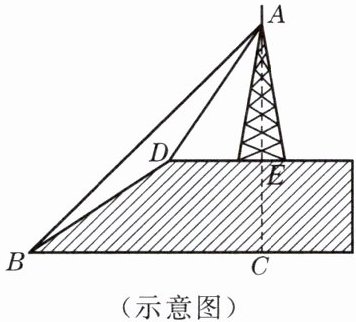

答案:
解:过点D作DF⊥BC于点F,
易得EC=DF,DE=FC.
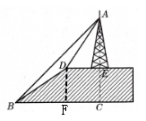
∵斜坡的坡比i=1:$\sqrt{3},$
∴$tan∠DBC=\frac {\sqrt{3}}{3},$
∴∠DBC=30°.
∵在Rt△DFB中∠DBC=30°,BD=50,
∴$DF=\frac {1}{2}BD=25,$
∴$BF=\sqrt{B{D}^2-D{F}^2}=25\sqrt{3}.$
∵在Rt△AED中∠ADE=60°,
AE=x,
∴$DE=\frac {AE}{tan∠ADE}=\frac {\sqrt{3}}{3}x.$
∵在Rt△ACB中∠ABC=45°,
∴AC=BC.设AE=x.
∵AC=AE+EC=x+25,
$BC=BF+FC=25\sqrt{3}+\frac {\sqrt{3}}{3}x,$
∴$x+25=25\sqrt{3}+\frac {\sqrt{3}}{3}x,$
∴$x=25\sqrt{3}≈43.3.$
答:铁架的高度AE为43.3米.
解:过点D作DF⊥BC于点F,
易得EC=DF,DE=FC.

∵斜坡的坡比i=1:$\sqrt{3},$
∴$tan∠DBC=\frac {\sqrt{3}}{3},$
∴∠DBC=30°.
∵在Rt△DFB中∠DBC=30°,BD=50,
∴$DF=\frac {1}{2}BD=25,$
∴$BF=\sqrt{B{D}^2-D{F}^2}=25\sqrt{3}.$
∵在Rt△AED中∠ADE=60°,
AE=x,
∴$DE=\frac {AE}{tan∠ADE}=\frac {\sqrt{3}}{3}x.$
∵在Rt△ACB中∠ABC=45°,
∴AC=BC.设AE=x.
∵AC=AE+EC=x+25,
$BC=BF+FC=25\sqrt{3}+\frac {\sqrt{3}}{3}x,$
∴$x+25=25\sqrt{3}+\frac {\sqrt{3}}{3}x,$
∴$x=25\sqrt{3}≈43.3.$
答:铁架的高度AE为43.3米.
10. 如图,海中有一个小岛 A,该岛四周 10 海里范围内有暗礁.有一货轮在海面上由西向东航行,到达 B 处时它在小岛南偏西55°的方向上,再往东行驶 20 海里后到达小岛的南偏西25°方向上的 C 处.如果货轮继续向东航行,是否会有触礁的危险?
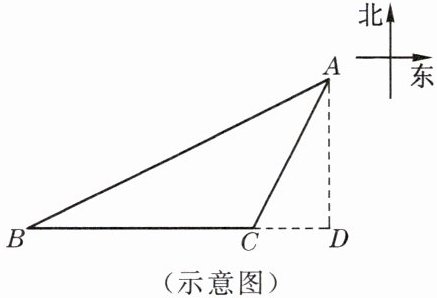

答案:
解:在Rt△ABD和Rt△ACD中,BD=AD·tan{55}°,CD=AD·tan{25}°.
∵BD-CD=BC,BC=20海里,
∴AD·tan{55}°-AD·tan{25}°=20,
∴AD·(tan{55}°-tan{25}°)=20,
∴$AD=\frac {20}{tan{55}°-tan{25}°}≈20.83($海里).
∵20.83>20,
∴如果货轮继续向东航行,不会有触礁的危险.
∵BD-CD=BC,BC=20海里,
∴AD·tan{55}°-AD·tan{25}°=20,
∴AD·(tan{55}°-tan{25}°)=20,
∴$AD=\frac {20}{tan{55}°-tan{25}°}≈20.83($海里).
∵20.83>20,
∴如果货轮继续向东航行,不会有触礁的危险.
查看更多完整答案,请扫码查看


