1. 如图,飞机 P 在目标 A 的正上方 1100 米处,飞行员测得目标 B 的俯角为 30°,求地面目标 A、B 之间的距离(结果保留根号).
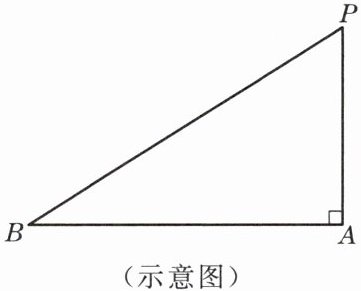
(示意图)

(示意图)
答案:
解:过P作PD//AB,则∠DPB=30°,如图所示:
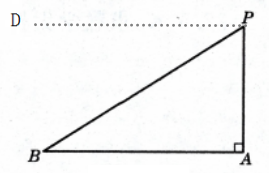
∵PD//AB,
∴∠B=∠DPB=30°,
∵∠A=90°
∴$tan∠B=\frac {AP}{AB}.$
∵∠B=30°,$tan∠B=\frac {AP}{AB},$AP=1100,
∴$AB=1100\sqrt{3}$米.
解:过P作PD//AB,则∠DPB=30°,如图所示:

∵PD//AB,
∴∠B=∠DPB=30°,
∵∠A=90°
∴$tan∠B=\frac {AP}{AB}.$
∵∠B=30°,$tan∠B=\frac {AP}{AB},$AP=1100,
∴$AB=1100\sqrt{3}$米.
2. 如图,湖心岛上有一凉亭 B,在凉亭 B 的正东湖边有一棵大树 A. 在湖边的 C 处测得 B 在北偏西 45°方向上,测得 A 在北偏东 32°方向上,又测得 A、C 之间的距离为 100 米. 求 A、B 之间的距离(精确到 1 米).
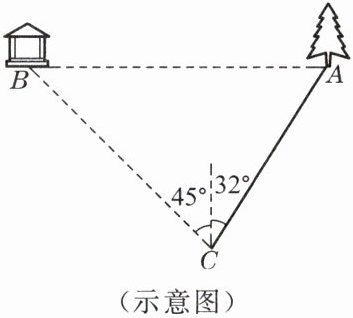
(示意图)

(示意图)
答案:
解:如图,过点C作CD⊥AB于点D.
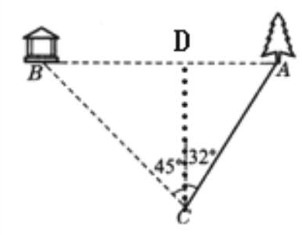
∵点B在点A的正东方向上,
∴∠ACD=32°,∠BCD=45°.
在Rt△ACD中,AC=100,
∴AD=AC×sin∠ACD=100×sin{32}°≈52.99.
CD=AC×cos∠ACD=100×cos{32}°≈84.8.
在Rt△BCD中,∠BCD=45°,
∴BD=CD,
∴AB=AD+BD≈84.8+52.99=137.79≈138,
即A,B之间的距离约为138米.
解:如图,过点C作CD⊥AB于点D.

∵点B在点A的正东方向上,
∴∠ACD=32°,∠BCD=45°.
在Rt△ACD中,AC=100,
∴AD=AC×sin∠ACD=100×sin{32}°≈52.99.
CD=AC×cos∠ACD=100×cos{32}°≈84.8.
在Rt△BCD中,∠BCD=45°,
∴BD=CD,
∴AB=AD+BD≈84.8+52.99=137.79≈138,
即A,B之间的距离约为138米.
查看更多完整答案,请扫码查看


