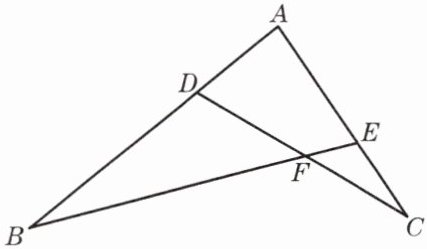
2. 已知:如图,点D、E分别在线段AB和AC上,AD·AB= AE·AC,点F是BE与CD的交点.
求证:△FDB∽△FEC.
求证:△FDB∽△FEC.

答案:
证明:
∵AD•AB=AE•AC,
∴$\frac {AD}{AE}=\frac {AC}{AB},$
∵∠A=∠A,
∴△ABE∽△ACD.
∴∠B=∠C,
∵∠DFB=∠EFC,
∴△DFB∽△EFC.
∵AD•AB=AE•AC,
∴$\frac {AD}{AE}=\frac {AC}{AB},$
∵∠A=∠A,
∴△ABE∽△ACD.
∴∠B=∠C,
∵∠DFB=∠EFC,
∴△DFB∽△EFC.
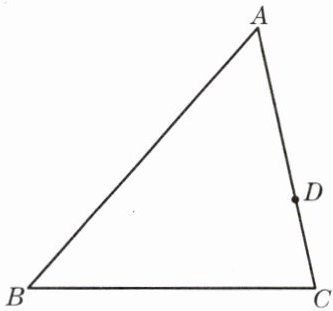
3. 如图,已知△ABC中,点D在边AC上,AB= 12厘米,AC= 8厘米,AD= 6厘米.当点P在边AB上的什么位置时,△ADP与△ABC相似?

答案:
解:当△ADP∽△ACB时,
∴$\frac {AP}{AD}=\frac {AB}{AC},$
∴$\frac {AP}{6}=\frac {12}{8},$
解得:AP=9;
当△ADP∽△ABC时,
∴$\frac {AP}{AD}=\frac {AC}{AB},$
∴$\frac {AP}{6}=\frac {8}{12},$
解得:AP=4.
∴当AP的长度为4或9时,△ADP和△ABC相似.
∴$\frac {AP}{AD}=\frac {AB}{AC},$
∴$\frac {AP}{6}=\frac {12}{8},$
解得:AP=9;
当△ADP∽△ABC时,
∴$\frac {AP}{AD}=\frac {AC}{AB},$
∴$\frac {AP}{6}=\frac {8}{12},$
解得:AP=4.
∴当AP的长度为4或9时,△ADP和△ABC相似.
1. 已知一个三角形的三边之比为 2∶3∶4,与它相似的另一个三角形的最大边长为 20 厘米,那么另一个三角形其他两边的长分别是
10
厘米和15
厘米.
答案:
10
15
15
查看更多完整答案,请扫码查看


