《2025年练习部分九年级数学上册沪教版54制》

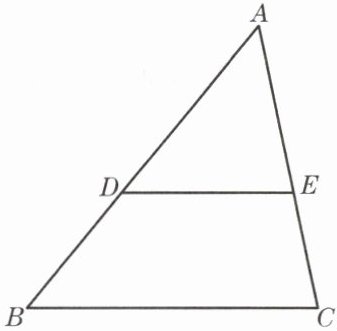
4. 如图,已知点D、E分别在△ABC的边AB和AC上,DE//BC,S△ADE：S四边形DBCE= 1：2. 求AD：DB.

答案： 解：
∵DE//BC，
∴△ADE∽△ABC.
∵$S_{△ADE}：S_{四边形DBCE}=1：2，$
∴$S_{△ADE}：S_{△ABC}=1：3，$
∴AD：AB=1：$\sqrt{3}，$
∴AD：DB=1：$(\sqrt{3}-1)$

1. 已知两个相似三角形的一组对应边长分别是35厘米和14厘米.
(1)如果它们的周长相差60厘米,求这两个三角形的周长.
(2)如果它们的面积相差420平方厘米,求这两个三角形的面积.

答案： 解：
(1)设大的三角形的周长为x厘米，则小的三角形的周长为(x-60)厘米，
根据相似三角形的周长比等于相似比可得
$ \dfrac{x}{x-60}=\dfrac{35}{14}$
14x=35(x-60)
14x=35x-2100
35x-14x=2100
21x=2100
x=100
经检验x=100是原方程的根
则较小三角形的周长为x-60=100-60=40(厘米)
则这两个三角形的周长分别是100厘米，40厘米.
(2)设较大三角形的面积是y平方厘米，则较
小三角形的面积为(y-420)平方厘米，根据相
似三角形的面积比等于相似比的平方可得：
$\dfrac{y}{y-420}={(\dfrac{35}{14})}^2={(\dfrac{5}{2})}^2 $
$\dfrac{y}{y-420}=\dfrac{25}{4}$
4y=25(y-420)
4y=25y-10500
25y-4y=10500
21y=10500
y=500
经检验y=500是原方程的根
则较小三角形的面积为
500-420=80(平方厘米)
则这两个三角形的面积分别为500平方厘
米，80平方厘米。

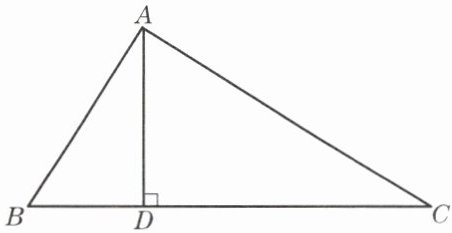
2. 如图,已知AD是Rt△ABC的斜边BC上的高,AC= 20,AB= 15. 求AD、BD、CD的长.

答案： 解：如图所示：
∵△ABC是直角三角形，AC=20，AB=15，
∴$BC=\sqrt {AB^2+AC^2}=\sqrt {15^2+20^2}=25．$
∵AD⊥BC，
∴$AD=\frac {AB•AC}{BC}=\frac {15×20}{25}=12．$
在Rt△ABD中，
∵AB=15，AD=12，
∴$BD=\sqrt {AB^2-AD^2}=\sqrt {15^2-12^2}=9，$
∴CD=BC-BD=25-9=16．