《2025年练习部分九年级数学上册沪教版54制》

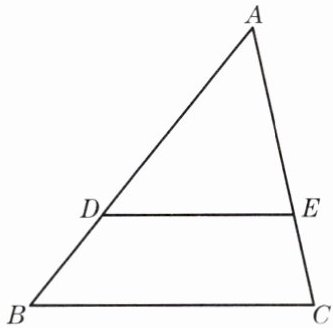
1. 如图,已知△ABC中,DE//BC,点D、E分别在边AB、AC上.
(1)如果AD= 5,DB= 3,AE= 4,求EC的长.
(2)如果AB= 9,AD= 6,AE= 4,求AC的长.
(3)如果AC= 12,EC= 4,DB= 5,求AB的长.

答案： 解：
(1)因为DE//BC
所以△ADE∽△ABC
所以$\frac {AD}{AB}=\frac {AE}{AC}$
所以$\frac {AB}{AD}=\frac {AC}{AE}$
所以$\frac {AB}{AD}-1=\frac {AC}{AE}-1$
所以$\frac {DB}{AD}=\frac {EC}{AE}$
因为AD=5，DB=3，AE=4
所以$\frac {3}{5}=\frac {EC}{4}$
所以$EC=\frac {12}{5}$
(2)因为△ADE∽△ABC
所以$\frac {AD}{AB}=\frac {AE}{AC}$
因为AB=9，AD=6，AE=4
所以$\frac {6}{9}=\frac {4}{AC}$
所以AC=6
解：
(3)因为△ADE∽△ABC
所以$\frac {AD}{AB}=\frac {AE}{AC}$
所以$1-\frac {AD}{AB}=1-\frac {AE}{AC}$
所以$\frac {DB}{AB}=\frac {EC}{AC}$
因为AC=12，EC=4，DB=5
所以$\frac {5}{AB}=\frac {4}{12}$
所以AB=15

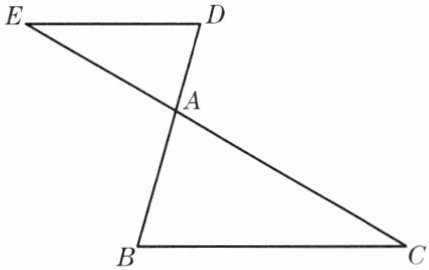
2. 如图,已知BD与CE相交于点A,ED//BC,AB= 8,AC= 12,AD= 6,求AE的长.

答案： 解：
∵AB=8，AD=6，
∴$\frac {AD}{AB}=\frac {3}{4}.$
∵ED//BC，
∴△ADE∽△ABC，
∴$\frac {AD}{AB}=\frac {AE}{AC}=\frac {3}{4}，$
∴$\frac {AE}{12}=\frac {3}{4}，$
∴AE=9.