1.二次函数$ y= -2(x-1)^2 $的图像的对称轴是
直线x=1
,顶点坐标是(1,0)
,开口方向是向下
.
答案:
直线x=1
(1,0)
向下
(1,0)
向下
2.填表:
| 函 数 | $ y= -3x^2 $ | $ y= -3(x+2)^2 $ | $ y= -3(x-2)^2 $ | $ y= -3(x+m)^2 $ |
| 抛物线的开口方向 | | | | |
| 抛物线的对称轴 | | | | |
| 抛物线的顶点坐标 | | | | |

| 函 数 | $ y= -3x^2 $ | $ y= -3(x+2)^2 $ | $ y= -3(x-2)^2 $ | $ y= -3(x+m)^2 $ |
| 抛物线的开口方向 | | | | |
| 抛物线的对称轴 | | | | |
| 抛物线的顶点坐标 | | | | |

答案:
向下
向下
向下
向下
y轴
直线x=-2
直线x=2
直线x=-m
(0,0)
(-2,0)
(2,0)
(-m,0)
向下
向下
向下
y轴
直线x=-2
直线x=2
直线x=-m
(0,0)
(-2,0)
(2,0)
(-m,0)
3.画函数$ y= 3(x-1)^2 $的图像,并写出图像的开口方向、对称轴和顶点坐标.
答案:
解:函数图象如下:
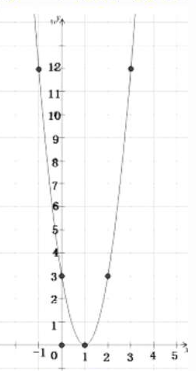
二次函数$y=3(x-1)^2$的图像的开口向上,顶点坐标为(1,0),对称轴为x=1.
解:函数图象如下:

二次函数$y=3(x-1)^2$的图像的开口向上,顶点坐标为(1,0),对称轴为x=1.
4.(1)把抛物线$ y= 2(x-1)^2 $向左平移4个单位,求所得新抛物线的表达式,并指出新抛物线的开口方向、对称轴和顶点坐标.
(2)把抛物线$ y= -3(x+2)^2 $向右平移3个单位,求所得新抛物线的表达式,并指出新抛物线的开口方向、对称轴和顶点坐标.
(2)把抛物线$ y= -3(x+2)^2 $向右平移3个单位,求所得新抛物线的表达式,并指出新抛物线的开口方向、对称轴和顶点坐标.
答案:
解:
(1)把抛物线$y=2(x-1)^2$向左平移4个单位,
所得新抛物线的表达式为$y=2(x+4-1)^2,$即$y=2(x+3)^2.$
抛物线$y=2(x+3)^2$的开口向上,对称轴为直线x=-3,顶点坐标为(-3,0).
(2)将抛物线向右平移3个单位,得到y=-3(x+2-3)²=-3(x-1)²
所以开口向下,对称轴为x=1,顶点坐标为(1,0)
(1)把抛物线$y=2(x-1)^2$向左平移4个单位,
所得新抛物线的表达式为$y=2(x+4-1)^2,$即$y=2(x+3)^2.$
抛物线$y=2(x+3)^2$的开口向上,对称轴为直线x=-3,顶点坐标为(-3,0).
(2)将抛物线向右平移3个单位,得到y=-3(x+2-3)²=-3(x-1)²
所以开口向下,对称轴为x=1,顶点坐标为(1,0)
查看更多完整答案,请扫码查看


