《2025年练习部分九年级数学上册沪教版54制》

2. 两个等腰三角形一定相似吗？顶角对应相等的两个等腰三角形相似吗？为什么？

答案： 解：两个等腰三角形不一定相似.因为两个等腰三角形的顶角不相等时，底角也一定
不相等，此时这两个等腰三角形不相似.
顶角相等的两个等腰三角形相似.

∵两个等腰三角形的顶角相等，

∴它们的底角都相等，

∴顶角相等的两个等腰三角形相似.

3. 已知：如图,正方形 ABCD 中,点 E 是边 CD 的中点,点 F 在边 BC 上,且 BC= 4CF. 求证：△ADE∽△ECF.

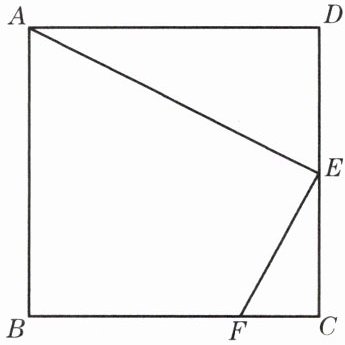
答案： 证明：因为四边形ABCD是正方形
所以∠D=∠C=90°，且AD=CD= BC
因为点E是边CD的中点
所以$CE= DE =\frac {1}{2}CD$
因为BC=4CF
所以$CF=\frac {1}{4}BC$
所以$\frac {DE}{CF}=2，$$\frac {AD}{EC}=2$
因为$\frac {DE}{CF}=\frac {AD}{EC}，$∠D=∠C
所以△ADE∽△ECF

4. 如图,方格纸上各方格的边长为 1 个单位,点 A、B、C、D 在小正方形顶点的位置上,试判断△ADB 与△ACD 是否相似,并说明理由.

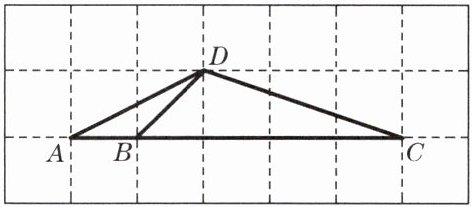
答案： 解：△ADB∽△ACD，理由如下：
根据勾股定理可得$AD=\sqrt{{1}^2+{2}^2}=\sqrt{5}.$
∵AB=1，AC=5，$AD=\sqrt{5}，$
∴$\frac {AD}{AC}=\frac {AB}{AD}.$
又
∵∠BAD=∠DAC，
∴△ADB∽△ACD.

1. 已知△ABC 和△DEF 中,AB= 2 厘米,BC= 3 厘米,CA= 4 厘米,DE= 7.5 厘米,EF= 10 厘米,FD= 5 厘米. 这两个三角形相似吗？为什么？

答案： 解：两个三角形相似，
理由：
∵$\frac {AB}{DF}=\frac {2}{5}，$$\frac {BC}{DE}=\frac {2}{5}，$$\frac {CA}{EF}=\frac {4}{10}=\frac {2}{5}，$
∴$\frac {AB}{DF}=\frac {BC}{DE}=\frac {CA}{EF}，$
∴△ABC∽△FDE．