《2025年练习部分九年级数学上册沪教版54制》

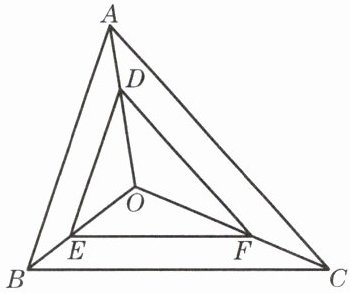
2. 已知:如图,点 $O$ 在 $\triangle ABC$ 的内部,点 $D$、$E$、$F$ 分别在线段 $OA$、$OB$、$OC$ 上,$\frac{OD}{OA}= \frac{OE}{OB}= \frac{OF}{OC}$.求证:$\triangle ABC \backsim \triangle DEF$.

答案： 证明：因为$\frac {OD}{OA}=\frac {OE}{OB}，$∠DOE=∠AOB
所以△DOE∽△AOB
所以$\frac {DE}{AB}=\frac {OD}{OA}$
因为$\frac {OD}{OA}=\frac {OF}{OC}，$∠DOF=∠AOC
所以△DOF∽△AOC
所以$\frac {DF}{AC}=\frac {OD}{OA}$
因为$\frac {OE}{OB}=\frac {OF}{OC}，$∠EOF=∠BOC
所以△EOF∽△BOC
所以$\frac {EF}{BC}=\frac {OE}{OB}$
所以$\frac {DE}{AB}=\frac {DF}{AC}=\frac {EF}{BC}$
所以△ABC∽△DEF.

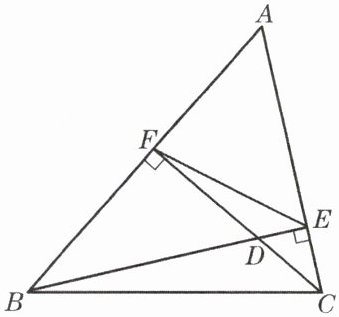
3. 已知:如图,$BE$、$CF$ 分别是 $\triangle ABC$ 的边 $AC$、$AB$ 上的高,$BE$ 与 $CF$ 相交于点 $D$.
(1) 求证:$\triangle ABC \backsim \triangle AEF$.
(2) 如果 $\angle A= 60^\circ$,求 $\frac{S_{\triangle AEF}}{S_{\triangle ABC}}$ 的值.

答案： 解：$(1)\because CF\bot AB，$$BE\bot AC$
$ \therefore \angle AEB=\angle AFC={90}^{\circ }$
$ \because \angle A=\angle A$
$ \therefore \triangle ABE\backsim \triangle ACF$
$ \therefore \dfrac{AE}{AF}=\dfrac{AB}{AC}$
$ \therefore \dfrac{AE}{AB}=\dfrac{AF}{AC}$
$ \because \angle A=\angle A$
$ \therefore \triangle ABC\backsim \triangle AEF$
(2)在$Rt\triangle ABE$中
$ \because \angle BAC={60}^{\circ }，$$\therefore \angle ABE={30}^{\circ }$
$ \therefore \dfrac{AE}{AB}=\dfrac{1}{2}$
$ \because \triangle AEF\backsim \triangle ABC，$
$ \therefore \dfrac{{S}_{\triangle AEF}}{{S}_{\triangle ABC}}={(\dfrac{AE}{AB})}^2={(\dfrac{1}{2})}^2=\dfrac{1}{4}$

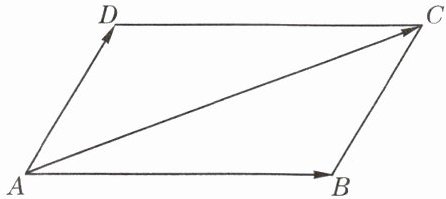
1. 如图,已知平行四边形ABCD,设$\overrightarrow{AB}= \overrightarrow{a}$,$\overrightarrow{AD}= \overrightarrow{b}$,在图中画出向量$\frac{2}{3}\overrightarrow{a}$,$-\frac{1}{2}\overrightarrow{b}$,$\frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})$.

答案：
解：如图

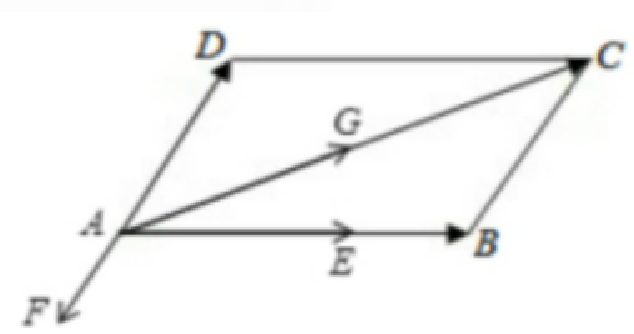
$ AE=\frac {2}{3}\overrightarrow{a}，$$AG=-\frac {1}{2}\overrightarrow{b}$
$ AG=\frac {1}{2}(\overrightarrow{a}+\overrightarrow{b})$