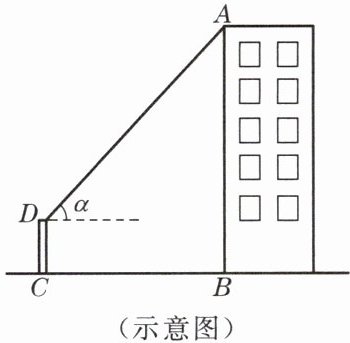
1. 为了测量学校教学大楼的高,在操场的点 C 处架起测角仪。测角仪的高 CD= 1.4 米,从点 D 测得教学大楼顶端 A 的仰角α= 42°15',测角仪底部 C 到大楼底部 B 的距离 CB= 22.5 米.求教学大楼的高(精确到 0.1 米).
(示意图)

(示意图)
答案:
解:过点D作DE⊥AB于点E,则DE=CB=22.5米,DC=BE=1.4米.
∵DE=22.5,∠ADE=40°15′,
∴AB=AE+BE=AE=DE×tan{40}°15′+1.4≈21.8米,
故教学大楼的高为21.8米.
解:过点D作DE⊥AB于点E,则DE=CB=22.5米,DC=BE=1.4米.
∵DE=22.5,∠ADE=40°15′,
∴AB=AE+BE=AE=DE×tan{40}°15′+1.4≈21.8米,
故教学大楼的高为21.8米.
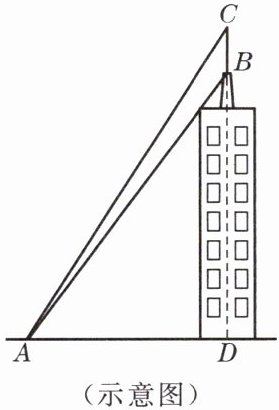
2. 为了测量大楼顶上(居中)避雷针 BC 的长度,在地面上点 A 处测得避雷针底部 B 和顶部 C 的仰角分别为 55°58'和 57°.已知点 A 与楼底中间部位 D 的距离约为 80 米.求避雷针 BC 的长度(精确到 0.1 米).
(示意图)

(示意图)
答案:
解:根据已知可得BD=AD·tan{55}°58′≈118.5,
CD=AD·tan{57}°≈123.2,
∴BC=CD-BD=4.7(米)
CD=AD·tan{57}°≈123.2,
∴BC=CD-BD=4.7(米)
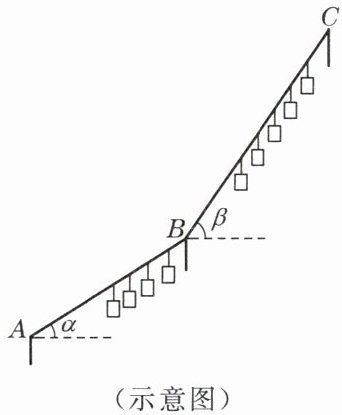
3. 登山缆车从山脚 A 到达山顶 C,中间要经过 B 处.从 A 处看点 B 处的仰角α= 28°,A、B 间的缆绳长 250 米;从 B 处看 C 处的仰角β= 42°,B、C 间的缆绳长 342 米.求山顶 C 和山脚 A 的高度差(精确到 1 米).
(示意图)

(示意图)
答案:
解:过点A作水平线AE,作BE⊥AE于点E,过点B作水平线BD,
作CD⊥BD于点D,如图.
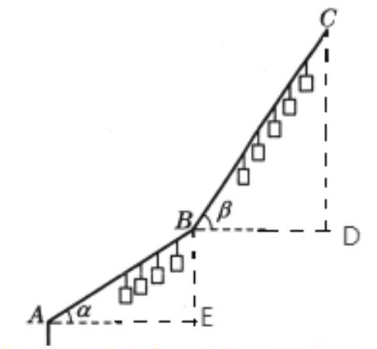
在Rt△BCD中,CD=BCsinβ=342×sin{42}°≈342×0.6691≈229(米);
在Rt△ABE中,BE=ABsinα=250×sin{28}°≈250×0.4695≈117(米),
∴山顶C和山脚A的高度差为CD+BE=346(米).
解:过点A作水平线AE,作BE⊥AE于点E,过点B作水平线BD,
作CD⊥BD于点D,如图.

在Rt△BCD中,CD=BCsinβ=342×sin{42}°≈342×0.6691≈229(米);
在Rt△ABE中,BE=ABsinα=250×sin{28}°≈250×0.4695≈117(米),
∴山顶C和山脚A的高度差为CD+BE=346(米).
查看更多完整答案,请扫码查看


