1. 已知矩形ABCD的对角线AC与BD相交于点O,如果$\overrightarrow{BC}= 5\overrightarrow{a},\overrightarrow{DC}= 3\overrightarrow{b}$,那么(
A.$\overrightarrow{BO}= \frac{1}{2}(5\overrightarrow{a}-3\overrightarrow{b})$;
B.$\overrightarrow{BO}= \frac{1}{2}(5\overrightarrow{a}+3\overrightarrow{b})$;
C.$\overrightarrow{BO}= \frac{1}{2}(3\overrightarrow{b}-5\overrightarrow{a})$;
D.$\overrightarrow{BO}= (5\overrightarrow{a}-3\overrightarrow{b})$.
A
)A.$\overrightarrow{BO}= \frac{1}{2}(5\overrightarrow{a}-3\overrightarrow{b})$;
B.$\overrightarrow{BO}= \frac{1}{2}(5\overrightarrow{a}+3\overrightarrow{b})$;
C.$\overrightarrow{BO}= \frac{1}{2}(3\overrightarrow{b}-5\overrightarrow{a})$;
D.$\overrightarrow{BO}= (5\overrightarrow{a}-3\overrightarrow{b})$.
答案:
A
2. 已知点D、E分别在△ABC的边AB、AC上,且DE//BC,$\overrightarrow{AD}= \frac{1}{3}\overrightarrow{AB}$.设$\overrightarrow{AB}= \overrightarrow{a},\overrightarrow{AC}= \overrightarrow{b}$,试用向量$\overrightarrow{a}、\overrightarrow{b}表示向量\overrightarrow{AD}、\overrightarrow{AE}、\overrightarrow{BC}、\overrightarrow{EC}$.
答案:
解:因为$\overrightarrow{AD}=\frac {1}{3}\overrightarrow{AB},$$\overrightarrow{AB}=\overrightarrow{a}$
所以$\overrightarrow{AD}=\frac {1}{3}\overrightarrow{a}$
因为DE//BC
所以$\overrightarrow{AE}=\frac {1}{3}\overrightarrow{AC}=\frac {1}{3}\overrightarrow{b}$
$ \overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{b}-\overrightarrow{a}$
$ \overrightarrow{EC}=\frac {2}{3}\overrightarrow{b}$
所以$\overrightarrow{AD}=\frac {1}{3}\overrightarrow{a}$
因为DE//BC
所以$\overrightarrow{AE}=\frac {1}{3}\overrightarrow{AC}=\frac {1}{3}\overrightarrow{b}$
$ \overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{b}-\overrightarrow{a}$
$ \overrightarrow{EC}=\frac {2}{3}\overrightarrow{b}$
3. 已知向量关系式$\frac{1}{3}(\overrightarrow{a}-\overrightarrow{x})= 2\overrightarrow{b}+6\overrightarrow{x}$,试用向量$\overrightarrow{a}、\overrightarrow{b}表示向量\overrightarrow{x}$.
答案:
解:因为$\frac {1}{3}(\overrightarrow{a}-\overrightarrow{x})=2\overrightarrow{b}+6\overrightarrow{x}$
所以$\frac {1}{3}\overrightarrow{a}-\frac {1}{3}\overrightarrow{x}=2\overrightarrow{b}+6\overrightarrow{x}$
所以$\frac {19}{3}\overrightarrow{x}=\frac {1}{3}\overrightarrow{a}-2\overrightarrow{b}$
所以$\overrightarrow{x}=\frac {1}{19}\overrightarrow{a}-\frac {6}{19}\overrightarrow{b}$
所以$\frac {1}{3}\overrightarrow{a}-\frac {1}{3}\overrightarrow{x}=2\overrightarrow{b}+6\overrightarrow{x}$
所以$\frac {19}{3}\overrightarrow{x}=\frac {1}{3}\overrightarrow{a}-2\overrightarrow{b}$
所以$\overrightarrow{x}=\frac {1}{19}\overrightarrow{a}-\frac {6}{19}\overrightarrow{b}$
4. 如图,已知向量$\overrightarrow{a}、\overrightarrow{b}$,求作向量:
(1)$(\frac{3}{2}\overrightarrow{a}-\overrightarrow{b})+3\overrightarrow{b}$.
(2)$(\frac{3}{2}\overrightarrow{a}-2\overrightarrow{b})-2(\overrightarrow{a}-\frac{1}{4}\overrightarrow{b})$.
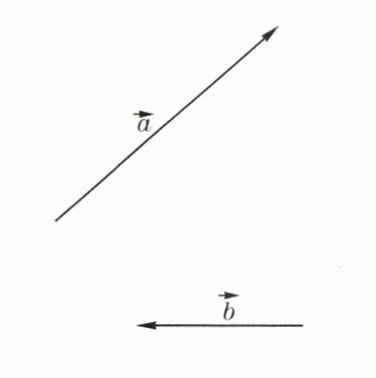
(1)$(\frac{3}{2}\overrightarrow{a}-\overrightarrow{b})+3\overrightarrow{b}$.
(2)$(\frac{3}{2}\overrightarrow{a}-2\overrightarrow{b})-2(\overrightarrow{a}-\frac{1}{4}\overrightarrow{b})$.

答案:
解:
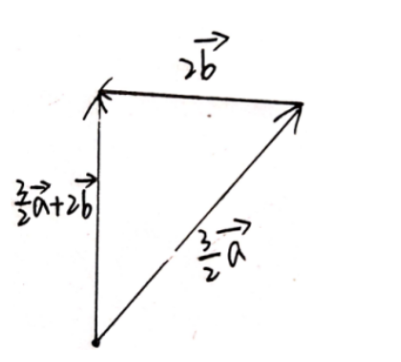
(1)原式$=\frac {3}{2}\overrightarrow{a}+2\overrightarrow{b}$
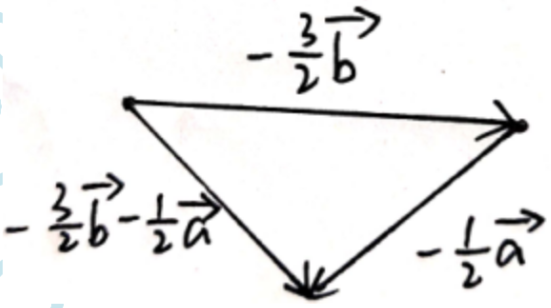
(2)原式$=\frac {3}{2}\overrightarrow{a}-2\overrightarrow{b}-2\overrightarrow{a}+\frac {1}{2}\overrightarrow{b}$
$ =-\frac {1}{2}\overrightarrow{a}-\frac {3}{2}\overrightarrow{b}$
解:
(1)原式$=\frac {3}{2}\overrightarrow{a}+2\overrightarrow{b}$

(2)原式$=\frac {3}{2}\overrightarrow{a}-2\overrightarrow{b}-2\overrightarrow{a}+\frac {1}{2}\overrightarrow{b}$
$ =-\frac {1}{2}\overrightarrow{a}-\frac {3}{2}\overrightarrow{b}$

查看更多完整答案,请扫码查看


