《2025年练习部分九年级数学上册沪教版54制》

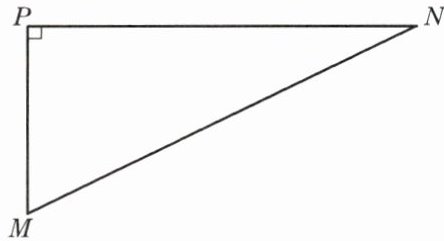
1. 如图,已知△MNP中,∠P= 90°,MP= 1,NP= 2. 求tanM、tanN、cotM、cotN的值.

答案： 解：
∵∠P=90°，MP=1，NP=2，


∴$tanM=\frac {NP}{MP}=\frac {2}{1}=2，$
$ tanN=\frac {MP}{NP}=\frac {1}{2}，$
$ cotM=\frac {MP}{NP}=\frac {1}{2}，$
$ cotN=\frac {NP}{MP}=\frac {2}{1}=2.$

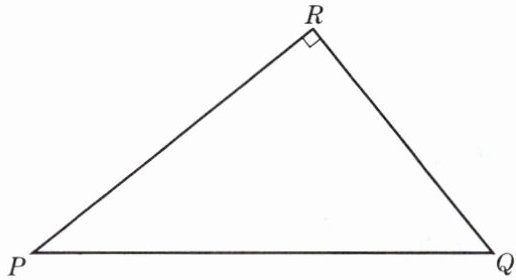
2. 如图,已知△PQR中,∠R= 90°,PR= 8,PQ= 10. 求tanP、cotP的值.

答案： 解：
∵∠R=90°，PR=8，PQ=10，

∴$RQ=\sqrt{P{Q}^2-P{R}^2}=\sqrt{1{0}^2-{8}^2}=6.$
$ tanP=RQ÷PR=6÷8=\frac {3}{4}，$
$ cotP=PR÷RQ=8÷6=\frac {4}{3}.$

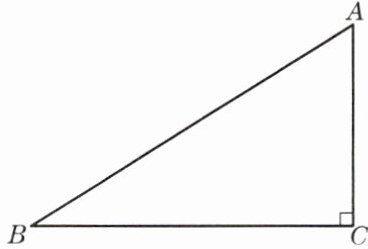
3. 如图,已知△ABC中,∠C= 90°. 设AC= a(a＞0),∠A= α,∠B= β.
(1) 用含a和α的式子表示BC的长.
(2) 用含a和β的式子表示BC的长.

答案： 解：
(1)
∵△ABC中，∠C=90°，AC=a，∠A=α，

∴$tanA=\frac {BC}{AC}=\frac {BC}{a}，$

∴BC=a·tanA=atanα.
(2)
∵△ABC中，∠C=90°，AC=a，∠B=β，

∴$cotB=\frac {BC}{AC}=\frac {BC}{a}，$

∴BC=a·cotB=acotβ.