《2025年练习部分九年级数学上册沪教版54制》

2. 如图,△ABC 和△DEF 在4×4的正方形网格中,它们的顶点都在边长为1的小正方形的顶点位置. 试判断△ABC 与△DEF 是否相似,并证明你的结论.

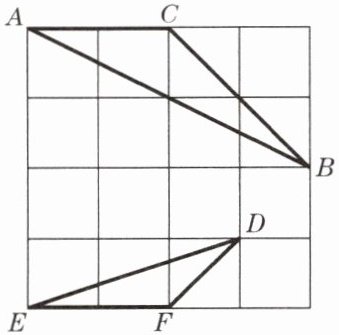
答案：


解：△ABC∽△DEF．理由如下：
在正方形方格中，$BC=\sqrt{{2}^2+{2}^2}=2\sqrt{2}，$
$ AB=\sqrt{{2}^2+{4}^2}=2\sqrt{5}，$
$ DF=\sqrt{{1}^2+{1}^2}=\sqrt{2}，$
$ DE=\sqrt{{1}^2+{3}^2}=\sqrt{10}．$
又AC=EF=2，
∴$\frac {AB}{DE}=\frac {BC}{FE}=\frac {AC}{DF}=\sqrt{2}，$
∴△ABC∽△DEF．

3. 已知：如图,AD、A_1D_1分别是△ABC 与△A_1B_1C_1的中线,且$\frac{AB}{A_1B_1}= \frac{BC}{B_1C_1}= \frac{AD}{A_1D_1}$. 求证：$\triangle ABC \sim \triangle A_1B_1C_1$.

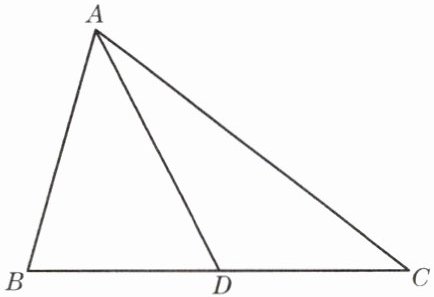
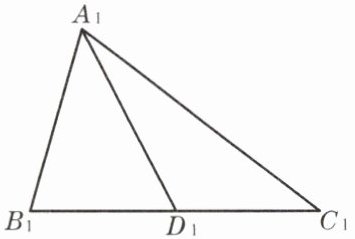
答案：
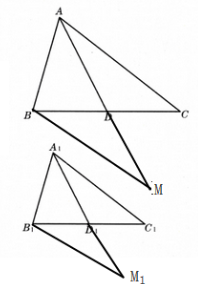
证明：如图，等倍延长中线AD、$A_1D_1$至M和$M_1，$连接BM和$B_1M_1，$

∵AD=DM，∠ADC=∠BDM，BD=CD，
∴△ADC≌△BDM.
同理可证$△A_1D_1C_1≌△M_1D_1B_1.$
∴BM=AC，$B_1M_1=A_1C_1.$
∵$\frac {AB}{{A}_1{B}_1}=\frac {AC}{{A}_1{C}_1}=\frac {AD}{{A}_1{D}_1}，$
∴$\frac {AB}{{A}_1{B}_1}=\frac {BM}{{B}_1{M}_1}=\frac {AM}{{A}_1{M}_1}，$
∴$△ABM∽△A_1B_1M_1，$
∴$∠BAM=∠B_1A_1M_1，$$∠M=∠M_1.$
由△ADC≌△MDB，得∠DAC=∠M，
由$△A_1D_1C_1≌△M_1D_1B_1$得$∠D_1A_1C_1=∠M_1，$
∴$∠DAC=∠D_1A_1C_1，$
∴$∠BAC=∠B_1A_1C_{1.}$
又
∵$\frac {AB}{{A}_1{B}_1}=\frac {AC}{{A}_1{C}_1}，$
∴$△ABC∽△A_1B_1C_1.$

1. 已知:如图,在 Rt△ABC 中,∠C= 90°,点 D 在边 BC 上,且$\frac{AB}{DA}= \frac{BC}{AC}$. 求证:∠B= ∠DAC.

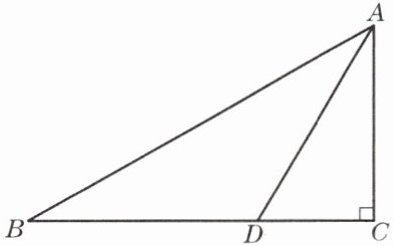
答案： 解：在Rt△ABC与Rt△ADC中，
∵$\frac {AB}{DA}=\frac {BC}{AC}，$
∴Rt△ABC∽Rt△ADC，
∴∠B=∠DAC．