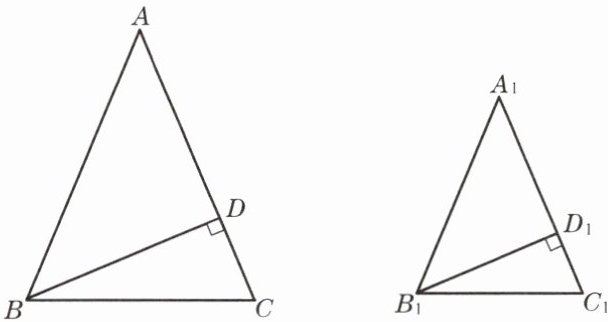
2. 已知:如图,在△ABC 与△A_1B_1C_1中,AB= AC,A_1B_1= A_1C_1,BD⊥AC,B_1D_1⊥A_1C_1,垂足分别为点 D、D_1,且$\frac{BD}{B_1D_1}= \frac{BC}{B_1C_1}$. 求证:△ABC∽△A_1B_1C_1.

答案:
$ $证明:因为$BD⊥AC,$$B_{1}D_{1}⊥A_{1}C_{1}$
$ $所以在$Rt△BCD$与$Rt△B_{1}C_{1}D_{1}$中,$$
$ $因为$\frac {BD}{B_{1}D_{1}}=\frac {BC}{B_{1}C_{1}}$
$ $所以$Rt△BCD∽Rt△B_{1}C_{1}D_{1}$
$ $所以$∠C=∠C_{1}$
$ $因为$AB= AC,$$A_{1}B_{1}=A_{1}C$
$ $所以$∠ABC=∠C,$$∠A_{1}B_{1}C_1=∠C_{1}$
$ $所以$∠ABC= ∠A_{1}B_{1}C_{1},$$∠C=∠C_{1}$
$ $所以$△ABC∽△A_1B_1C_1.$
$ $所以在$Rt△BCD$与$Rt△B_{1}C_{1}D_{1}$中,$$
$ $因为$\frac {BD}{B_{1}D_{1}}=\frac {BC}{B_{1}C_{1}}$
$ $所以$Rt△BCD∽Rt△B_{1}C_{1}D_{1}$
$ $所以$∠C=∠C_{1}$
$ $因为$AB= AC,$$A_{1}B_{1}=A_{1}C$
$ $所以$∠ABC=∠C,$$∠A_{1}B_{1}C_1=∠C_{1}$
$ $所以$∠ABC= ∠A_{1}B_{1}C_{1},$$∠C=∠C_{1}$
$ $所以$△ABC∽△A_1B_1C_1.$
3. 如图,已知梯形 ABCD 中,AD$//$BC,∠A= 90°,AD= 2,BC= 3,AB= 7,P 是边 AB 上的一点. 当点 P 在何处时,△APD 与△BPC 相似?


答案:
解:若△ADP∽△BCP,则$\frac {AP}{BP}=\frac {AD}{BC},$
∵AD=2,BC=3,AB=7,
∴$\frac {AP}{7-AP}=\frac {2}{3},$
解得AP=2.8;
若△ADP∽△BPC,则$\frac {AP}{BC}=\frac {AD}{BP},$
即$\frac {AP}{3}=\frac {2}{7-AP},$
解得AP=1或6.
∴当AP的长为1或2.8或6时,△APD与△BPC相似.
∵AD=2,BC=3,AB=7,
∴$\frac {AP}{7-AP}=\frac {2}{3},$
解得AP=2.8;
若△ADP∽△BPC,则$\frac {AP}{BC}=\frac {AD}{BP},$
即$\frac {AP}{3}=\frac {2}{7-AP},$
解得AP=1或6.
∴当AP的长为1或2.8或6时,△APD与△BPC相似.
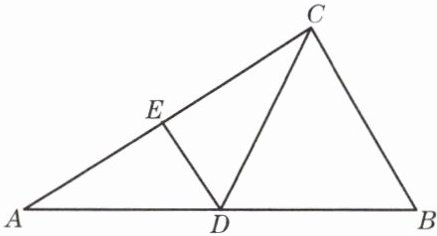
1. 已知:如图,在△ABC中,∠ACB= 90°,D、E分别是边AB、AC的中点.
求证:△ABC∽△CDE.
求证:△ABC∽△CDE.

答案:
证明:因为D、E分别是边AB、AC的中点,
所以DE是△ABC的中位线,
所以DE//BC.
因为∠ACB=90°,
所以∠CED=90°.因为E是AC的中点
所以△ACD是等腰三角形,所以∠A=∠ECD
因为∠A=∠ECD,∠ACB=∠CED,
所以△ABC∽△CDE.
所以DE是△ABC的中位线,
所以DE//BC.
因为∠ACB=90°,
所以∠CED=90°.因为E是AC的中点
所以△ACD是等腰三角形,所以∠A=∠ECD
因为∠A=∠ECD,∠ACB=∠CED,
所以△ABC∽△CDE.
查看更多完整答案,请扫码查看


