《2024年练习部分九年级数学上册沪教版54制》

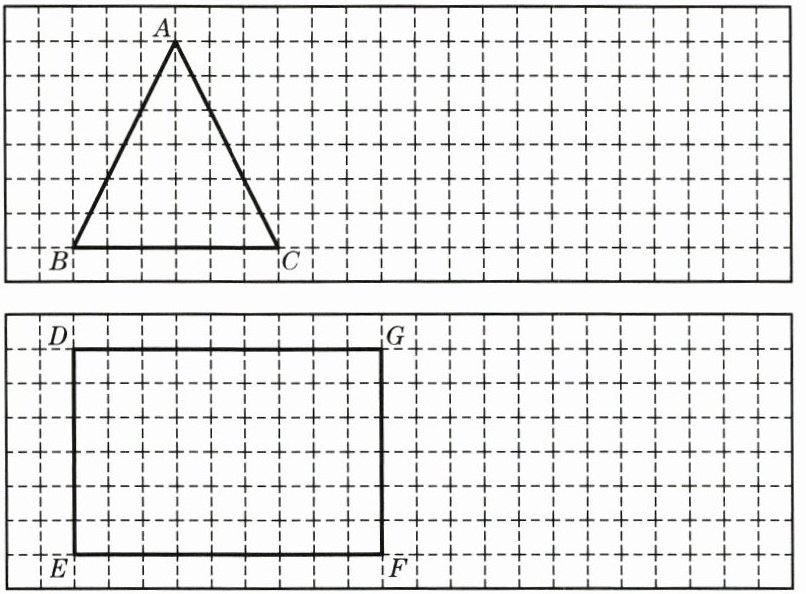
1. 在下列方格图中,分别画出一个与△ABC、四边形DEFG相似的图形.

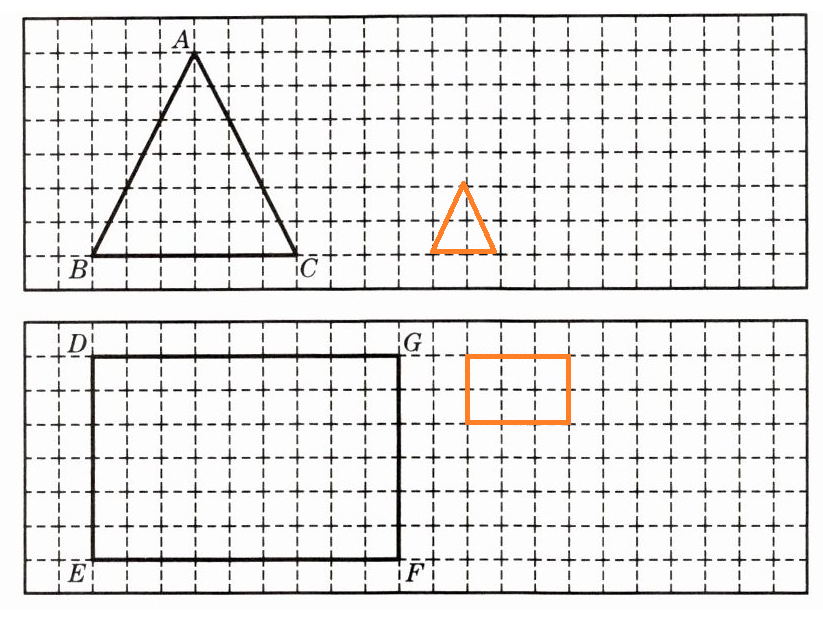
答案：

2. 已知△ABC与△A′B′C′相似,并且点A与点A′、点B与点B′、点C与点C′是对应顶点,其中AB、BC、CA的长分别为6厘米、8厘米、10厘米,A′B′的长为4厘米,求B′C′、C′A′的长.

答案： $解：因为△ABC∽△A'B'C'$
$所以\frac {AB}{A'B'}=\frac {BC}{B'C'}=\frac {CA}{C'A'}$
$所以\frac {6}{4}=\frac {8}{B'C'}=\frac {10}{C'A'}$
$解得B'C'=\frac {16}{3}厘米，C'A'=\frac {20}{3}厘米.$

3. (1)四个内角都对应相等的两个四边形一定相似吗？为什么？
(2)所有的等边三角形都一定相似吗？所有的菱形呢？为什么？

答案： $解：(1)四个内角都对应相等的两个四边形不一定相似.$
$因为两个四边形的对应边不一定成比例.$
$(2)所有的等边三角形的各个内角都是60°，$
$ 根据相似三角形的判定定理：有两个角对应相等的三角形相似，可得所有的等边$
$三角形一定相似.$
$ 所有的菱形不一定相似，如一般菱形和特殊的菱形(正方形)不可能相似，即对应角$
$不相等，所以所有的菱形不一定相似.$