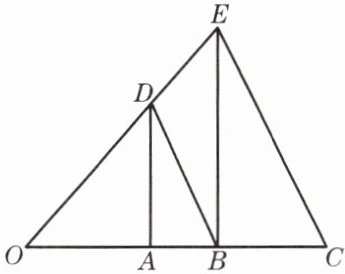
8. 已知:如图,在$\triangle OCE$中,点 A、B 在边 OC 上,点 D 在边 OE 上,$OB^2= OA\cdot OC$,$AD// BE$.求证:$DB// EC$.

答案:
证明:因为AD//BE
所以$\frac {OA}{OB}=\frac {OD}{OE}$
因为OB²=OA×OC
所以$\frac {OA}{OB}=\frac {OB}{OC}$
所以$\frac {OB}{OC}=\frac {OD}{OE}$
因为∠O=∠O
所以△OBD∽△OCE
所以DB//EC.
所以$\frac {OA}{OB}=\frac {OD}{OE}$
因为OB²=OA×OC
所以$\frac {OA}{OB}=\frac {OB}{OC}$
所以$\frac {OB}{OC}=\frac {OD}{OE}$
因为∠O=∠O
所以△OBD∽△OCE
所以DB//EC.
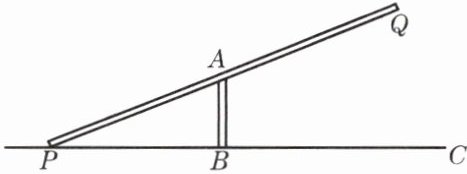
9. 跷跷板 PQ 的直立支柱 AB 的高度为 0.4 米,直线 BC 表示地面.(1)当支点 A 为跷跷板 PQ 的中点时,跷跷板的一端 Q 可达到的最大高度是多少米?(2)平移支柱 AB 的位置,使跷跷板的一端 Q 的最大高度达到 1.0 米,这时支点 A 分 PQ 所成两段中较长一段与较短一段的长度的比值是多少?

答案:
解:
(1)如图,过点Q作QH⊥BC.
∵支点A为跷跷板PQ的中点,AB//QH,
∴AB为△PHQ的中位线.
∵AB=0.4米,
∴QH=2AB=0.8米.
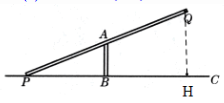
(2)如图,过点Q作QH⊥BC.
∵AB//QH,
∴△PAB∽△PQH,
∴$\frac {AB}{QH}=\frac {PA}{PQ}=\frac {0.4}{1}=\frac {2}{5},$
∴$\frac {AQ}{PA}=\frac {3}{2},$
∴支点A分Q所成两段中较长一段与较短一段的长度的比值是3:2.
解:
(1)如图,过点Q作QH⊥BC.
∵支点A为跷跷板PQ的中点,AB//QH,
∴AB为△PHQ的中位线.
∵AB=0.4米,
∴QH=2AB=0.8米.
(2)如图,过点Q作QH⊥BC.
∵AB//QH,
∴△PAB∽△PQH,
∴$\frac {AB}{QH}=\frac {PA}{PQ}=\frac {0.4}{1}=\frac {2}{5},$
∴$\frac {AQ}{PA}=\frac {3}{2},$
∴支点A分Q所成两段中较长一段与较短一段的长度的比值是3:2.

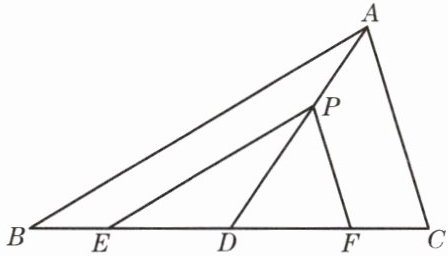
10. 已知:如图,P 是$\triangle ABC$的中线 AD 上的一点,$PE// AB$,$PF// AC$,PE、PF 分别与 BC 相交于点 E、F.求证:$BE= CF$.

答案:
证明:
∵PE//AB,
∴$\frac {DP}{AD}=\frac {DE}{BD}.$
∵PF//AC,
∴$\frac {DP}{AD}=\frac {DF}{CD}.$
∵AD为△ABC的中线,
∴BD=CD,
∴DE=DF,
∴BD-DE=CD-DF,
即BE=CF.
∵PE//AB,
∴$\frac {DP}{AD}=\frac {DE}{BD}.$
∵PF//AC,
∴$\frac {DP}{AD}=\frac {DF}{CD}.$
∵AD为△ABC的中线,
∴BD=CD,
∴DE=DF,
∴BD-DE=CD-DF,
即BE=CF.
查看更多完整答案,请扫码查看


