《2025年练习部分九年级数学上册沪教版54制》

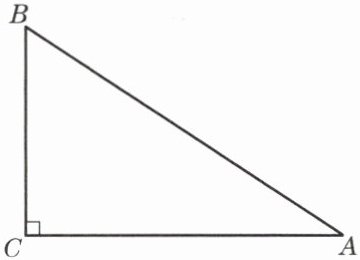
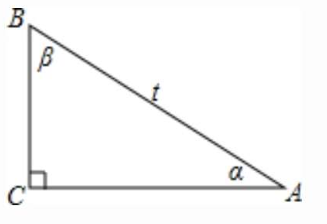
3. 如图,已知△ABC中,∠C= 90°,AB= t(t＞0),∠A= α,∠B= β.
(1)用 t 和 α 的三角比分别表示 AC、BC 的长.
(2)用 t 和 β 的三角比分别表示 AC、BC 的长.

答案：

解：
(1)
∵sinA=ABCB​，cosA=ABAC​，
∴BC=AB×sinA=tsinα，
AC=AB×cosA=tcosα.
(2)
∵cosB=ABBC​，sinB=ABAC​，
∴BC=AB×cosB=tcosβ，
AC=AB×sinB=tsinβ．

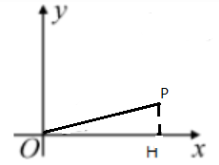
4. 在直角坐标平面内,已知点 P(4,1),点 P 与原点 O 的连线与 x 轴的正半轴的夹角为 α. 求 tanα、cotα、sinα、cosα 的值.

答案：
解：如图，过点P作PH⊥x轴，垂足为H，
∵P(4，1)，
∴OH=4，PH=1，
∴$OP=\sqrt{{4}^2+{1}^2}=\sqrt{17}，$
∴$tanα=\frac {PH}{OH}=\frac {1}{4}，$
$ cotα=\frac {OH}{PH}=4，$
$ sinα=\frac {PH}{OP}=\frac {1}{\sqrt{17}}=\frac {\sqrt{17}}{17}，$
$ cosα=\frac {OH}{OP}=\frac {4}{\sqrt{17}}=\frac {4\sqrt{17}}{17}.$

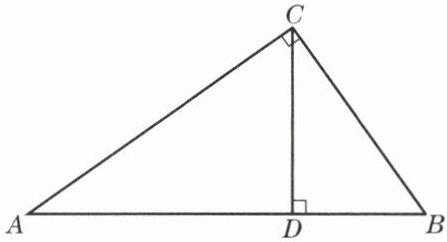
5. 如图,已知△ABC中,∠ACB= 90°,AC= 4,BC= 3,CD⊥AB,垂足为点 D,求 sin∠ACD 的值. 能用两种不同的方法求解吗？

答案： 解：方法一：
∵∠ACB=90°，BC=3，AC=4，
∴$AB=\sqrt{B{C}^2+A{C}^2}=\sqrt{{3}^2+{4}^2}=5，$
∵CD⊥AB，
∴∠ADC=∠BDC=90°，
∵∠ACD+∠BCD=90°，∠A+∠ACD=90°，∠B+∠BCD=90°，
∴∠ACD=∠B，∠BCD=∠A，
∴$sin∠ACD=sin∠B=\frac {AC}{AB}=\frac {4}{5}.$
方法二：
∵∠ACB=90°，BC=3，AC=4，
∴$AB=\sqrt{B{C}^2+A{C}^2}=\sqrt{{3}^2+{4}^2}=5，$设BD=x，则AD=5-x，
∵∠ACB=90°，CD⊥AB，
∴$4^2-(5-x)^2=3^2-x^2$
解得x=1.8
∴AD=5-1.8=3.2，
∴$sin∠ACD=\frac {AD}{AC}=\frac {3.2}{4}=\frac {4}{5}.$