第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
1. 计算 $3 - (-3)$ 的结果等于( )
A.$-6$
B.$0$
C.$3$
D.$6$
A.$-6$
B.$0$
C.$3$
D.$6$
答案:
D
2. 比 $-2$ 小 $8$ 的数是______。
答案:
-10
3. 填空:
(1) ( ) $- (-4) = -9$。
(2) $9 - ($ ) $= 13$。
(3) ( ) $- (+3) = -7$。
(4) $-(-3) - 1 = ($ )。
(1) ( ) $- (-4) = -9$。
(2) $9 - ($ ) $= 13$。
(3) ( ) $- (+3) = -7$。
(4) $-(-3) - 1 = ($ )。
答案:
(1)-13
(2)-4
(3)-4
(4)2
(1)-13
(2)-4
(3)-4
(4)2
4. 如图,$A$,$B$,$C$,$D$,$E$ 为未标出原点的数轴上的五个点,且相邻两点之间的距离相等,则点 $B$ 所表示的数是( )

A.$2$
B.$7$
C.$10$
D.$12$

A.$2$
B.$7$
C.$10$
D.$12$
答案:
A
5. 计算下列各题:
(1) $(-12) - (+8) - (+10) - (-8)$。
(2) $(+55) - (-9.4) - (+32) - (+9.4)$。
(3) $2\frac{2}{3} - (+1\frac{3}{4}) - (-3\frac{1}{3})$。
(4) $\frac{3}{4} - [\frac{4}{7} - (+0.25)]$。
(1) $(-12) - (+8) - (+10) - (-8)$。
(2) $(+55) - (-9.4) - (+32) - (+9.4)$。
(3) $2\frac{2}{3} - (+1\frac{3}{4}) - (-3\frac{1}{3})$。
(4) $\frac{3}{4} - [\frac{4}{7} - (+0.25)]$。
答案:
(1)原式=(-12)+(-8)+(-10)+(+8)
=-12-8-10+8
=-30+8
=-22.
(2)原式=(+55)+(+9.4)+(-32)+(-9.4)
=55+9.4-32-9.4
=55-32+9.4-9.4
=23.
(3)原式=$2\frac{2}{3}+(-1\frac{3}{4})+(+3\frac{1}{3})$
=$2\frac{2}{3}-1\frac{3}{4}+3\frac{1}{3}$
=$2\frac{2}{3}+3\frac{1}{3}-1\frac{3}{4}$
=6-$1\frac{3}{4}$
=$4\frac{1}{4}$.
(4)原式=$\frac{3}{4}-[\frac{4}{7}+(-\frac{1}{4})]$
=$\frac{3}{4}-(\frac{4}{7}-\frac{1}{4})$
=$\frac{3}{4}-\frac{4}{7}+\frac{1}{4}$
=$\frac{3}{4}+\frac{1}{4}-\frac{4}{7}$
=1-$\frac{4}{7}$
=$\frac{3}{7}$.
(1)原式=(-12)+(-8)+(-10)+(+8)
=-12-8-10+8
=-30+8
=-22.
(2)原式=(+55)+(+9.4)+(-32)+(-9.4)
=55+9.4-32-9.4
=55-32+9.4-9.4
=23.
(3)原式=$2\frac{2}{3}+(-1\frac{3}{4})+(+3\frac{1}{3})$
=$2\frac{2}{3}-1\frac{3}{4}+3\frac{1}{3}$
=$2\frac{2}{3}+3\frac{1}{3}-1\frac{3}{4}$
=6-$1\frac{3}{4}$
=$4\frac{1}{4}$.
(4)原式=$\frac{3}{4}-[\frac{4}{7}+(-\frac{1}{4})]$
=$\frac{3}{4}-(\frac{4}{7}-\frac{1}{4})$
=$\frac{3}{4}-\frac{4}{7}+\frac{1}{4}$
=$\frac{3}{4}+\frac{1}{4}-\frac{4}{7}$
=1-$\frac{4}{7}$
=$\frac{3}{7}$.
6. 圆圆想了解某地某天的天气情况,在某气象网站查询到该地这天的最低气温为 $-6^{\circ}C$,最高气温为 $2^{\circ}C$,则该地这天的温差(最高气温与最低气温的差)为( )

A.$-8^{\circ}C$
B.$-4^{\circ}C$
C.$4^{\circ}C$
D.$8^{\circ}C$

A.$-8^{\circ}C$
B.$-4^{\circ}C$
C.$4^{\circ}C$
D.$8^{\circ}C$
答案:
D
7. 阅读并解答问题:
《九章算术》——正负术
《九章算术》大约于东汉初年(公元 $1$ 世纪)成书,共九章,汇总了战国和西汉时期的数学成果,是几代人共同劳动的结晶,在世界数学史上首次正式引入负数及其加减法运算法则,给出名为“正负术”的算法。加法法则为:“异名相除,同名相益,正无入正之,负无入负之。”即异号两数相加,绝对值相减,同号两数相加,绝对值相加;$0$ 加正数和为正,$0$ 加负数和为负。类似地有减法法则:“同名相除,异名相益,正无入负之,负无入正之。”
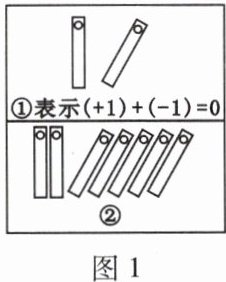
(1) 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数。如图 $1$,根据刘徽的这种表示法,观察图 $1$①,可推算图 $1$②中所得的结果为( )
A. $-3$
B. $+3$
C. $-6$
D. $+6$
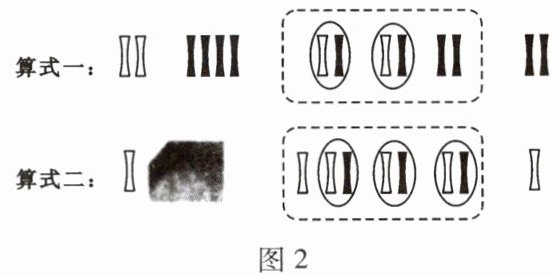
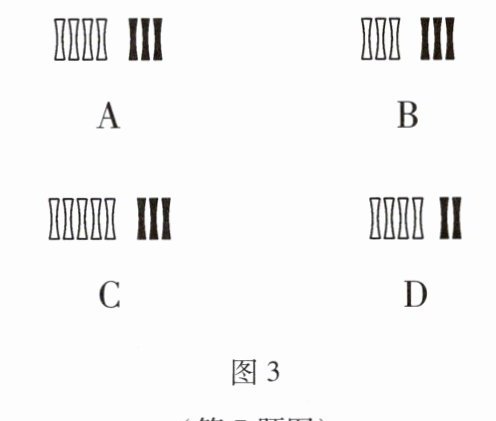
(2) 筹算是中国古代的计算方法之一,宋代数学家用白色筹码代表正数,用黑色筹码代表负数,如图 $2$ 中算式一表示的是 $(+2) + (-4) = -2$。按照这种算法,在图 $3$ 的四个选项中,图 $2$ 中算式二被盖住的部分是( )
《九章算术》——正负术
《九章算术》大约于东汉初年(公元 $1$ 世纪)成书,共九章,汇总了战国和西汉时期的数学成果,是几代人共同劳动的结晶,在世界数学史上首次正式引入负数及其加减法运算法则,给出名为“正负术”的算法。加法法则为:“异名相除,同名相益,正无入正之,负无入负之。”即异号两数相加,绝对值相减,同号两数相加,绝对值相加;$0$ 加正数和为正,$0$ 加负数和为负。类似地有减法法则:“同名相除,异名相益,正无入负之,负无入正之。”
(1) 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数。如图 $1$,根据刘徽的这种表示法,观察图 $1$①,可推算图 $1$②中所得的结果为( )
A. $-3$
B. $+3$
C. $-6$
D. $+6$
(2) 筹算是中国古代的计算方法之一,宋代数学家用白色筹码代表正数,用黑色筹码代表负数,如图 $2$ 中算式一表示的是 $(+2) + (-4) = -2$。按照这种算法,在图 $3$ 的四个选项中,图 $2$ 中算式二被盖住的部分是( )



答案:
(1)A
(2)B
(1)A
(2)B
查看更多完整答案,请扫码查看


