第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 如图,$∠ABC= ∠DCB$,若直接用“ASA”证明$\triangle ABC\cong \triangle DCB$,还需添加的条件为 (
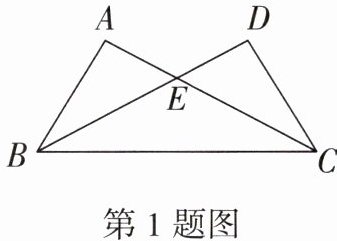
A.$AB= CD$
B.$BD= AC$
C.$∠AEB= ∠DEC$
D.$∠ACB= ∠DBC$
D
)
A.$AB= CD$
B.$BD= AC$
C.$∠AEB= ∠DEC$
D.$∠ACB= ∠DBC$
答案:
D
2. 如图,$∠B= ∠E,AC// FD,BF= CE$,点B,C,E,F在同一条直线上. 求证:$\triangle ABC\cong \triangle DEF.$


答案:
证明:
∵ AC//FD,
∴ ∠ACB=∠DFE,
∵ BF=CE,
∴ BF+FC=CE+FC,
∴ BC=EF,
在△ABC 和△DEF 中,∠B=∠E,
BC=EF,
∠ACB=∠DFE,
∴ △ABC≌△DEF(ASA).
∵ AC//FD,
∴ ∠ACB=∠DFE,
∵ BF=CE,
∴ BF+FC=CE+FC,
∴ BC=EF,
在△ABC 和△DEF 中,∠B=∠E,
BC=EF,
∠ACB=∠DFE,
∴ △ABC≌△DEF(ASA).
3. 如图,在$\triangle ABC$中,$AD⊥BC$于点D,$BE⊥AC$于点E,AD,BE相交于点H,且$AD= BD.$
求证:(1)$∠DBH= ∠DAC;$
(2)$\triangle BDH\cong \triangle ADC.$

求证:(1)$∠DBH= ∠DAC;$
(2)$\triangle BDH\cong \triangle ADC.$

答案:
证明:
(1)
∵ AD⊥BC,BE⊥AC,
∴ ∠ADC=∠BEC=90°,
∵ ∠C=∠C,
∴ ∠DBH=∠DAC;
(2)
∵ AD⊥BC,
∴ ∠ADB=∠ADC,
在△BDH 与△ADC 中,
∠BDH=∠ADC
BD=AD
∠DBH=∠DAC
,
∴ △BDH≌△ADC(ASA).
(1)
∵ AD⊥BC,BE⊥AC,
∴ ∠ADC=∠BEC=90°,
∵ ∠C=∠C,
∴ ∠DBH=∠DAC;
(2)
∵ AD⊥BC,
∴ ∠ADB=∠ADC,
在△BDH 与△ADC 中,
∠BDH=∠ADC
BD=AD
∠DBH=∠DAC
,
∴ △BDH≌△ADC(ASA).
4. 如图是一块三角形的玻璃被打碎后的三个部分,若只将其中某一部分带去玻璃店就能重新配一块大小、形状相同且完整的新玻璃,你会选 (
A.①号玻璃
B.②号玻璃
C.③号玻璃
D.①②号玻璃
C
)A.①号玻璃
B.②号玻璃
C.③号玻璃
D.①②号玻璃
答案:
C
5. (教材练习第2题改编)如图,点E,A,C在同一条直线上,$AB// CD,AC= CD,∠ACB= ∠D$,若$AB= 5,AC= 3$,则AE的长为
2
.
答案:
2
6. (教材复习题第11题改编)如图,在$\triangle ABC$中,$∠B= ∠C$,点D,E分别在边BC上,且$BD= CE,∠1= ∠2$,若$∠BAD= 25^{\circ },∠BAC= 80^{\circ }$,则$∠DAE$的度数为____
30°
.
答案:
30°
7. 日常生活情境 燕尾形风筝 小明准备制作如图①所示的燕尾形风筝骨架,如图②所示,他先将两根长度相同的竹条AB,AC扎在一起,再用竹条BE,CD进行固定,并使得$∠BDC= ∠CEB$,这样能保证$\triangle ABE\cong \triangle ACD$吗? 请说明理由.
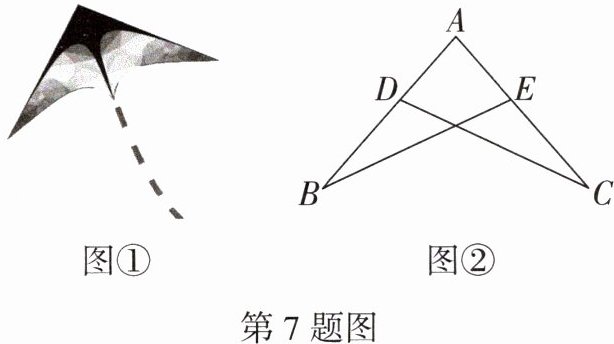

答案:
解:能保证△ABE≌△ACD. 理由如下:
由外角性质可知∠BDC=∠A+∠C,∠CEB=
∠A+∠B,
∵ ∠BDC=∠CEB,
∴ ∠B=∠C.
在△ABE 和△ACD 中,∠B=∠C,
AB=AC,
∠A=∠A,
∴ △ABE≌△ACD(ASA).
由外角性质可知∠BDC=∠A+∠C,∠CEB=
∠A+∠B,
∵ ∠BDC=∠CEB,
∴ ∠B=∠C.
在△ABE 和△ACD 中,∠B=∠C,
AB=AC,
∠A=∠A,
∴ △ABE≌△ACD(ASA).
查看更多完整答案,请扫码查看


