《2025年万唯中考情境题八年级数学上册苏科版》

10. 如图①是一个纸飞机,图②是其部分展开图,纸飞机两侧的部分关于折痕 AF 对称,则图中全等的三角形的对数是(D)
11. 如图①是一个纸风车,其深色部分如图②所示,由四个全等的直角三角形组成,已知 AB= 4 cm,CG= 6 cm,则深色部分的面积为24$cm^2$

答案： 10.D　11.24

12. 数学文化情境 赵爽弦图 如图,是我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,该图由四个全等的直角三角形和一个小正方形 EFGH 组成,恰好拼成一个大正方形 ABCD. 若 HG= 1,S_{△ABE}= 6,则正方形 ABCD 的边长为5.

答案： 5

13. (中考新考法·结论开放)用两种不同的方法沿网格线将如图所示的图形分割成两个全等的图形.

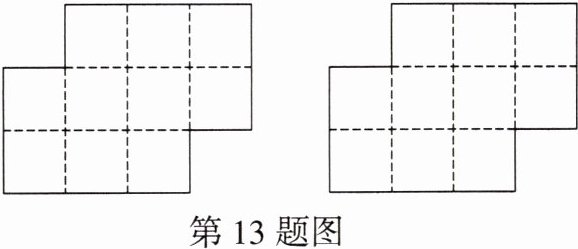
答案：
解:分割方法如解图所示(答案不唯一，作出其中两种即可).
　　　　

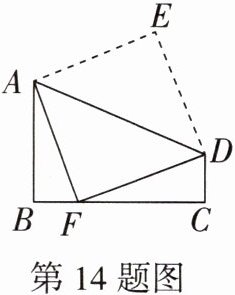
14. 如图,将五边形 ABCDE 沿 AD 折叠,点 E 的对应点 F 落在 BC 上,已知△ABF≌△FCD,∠B= 90°.
(1)判断线段 AF 与 FD 之间的数量关系及位置关系,并说明理由；
(2)若 AF= 8,求△AED 的面积.

答案：
(1)AF=FD且AF⊥FD.理由如下:
∵∠B=90°,
∴∠FAB+∠BFA=90°,
∵△ABF≌△FCD,
∴AF=FD,∠FAB=∠DFC,
∴∠BFA+∠DFC=90°,
∴∠AFD=90°,
∴AF⊥FD;
(2)由
(1)得AF⊥FD,AF=FD=8,
∴$S_{\triangle AFD}=\frac{1}{2}AF\cdot FD=\frac{1}{2}×8×8=32$,
　　由折叠的性质得$S_{\triangle AED}=S_{\triangle AFD}=32$.

15. 如图,AB//CD,连接 BC,点 E,F 分别在 BC,CD 上,连接 AE,EF,已知 AB= CD= 12,BC= 16,点 E 沿线段 BC 以每秒 4 个单位长度的速度从点 B 出发,向点 C 移动,同时点 F 从点 C 出发,沿线段 CD 向点 D 移动,设运动时间为 t 秒(0＜t＜4),当△ABE 和△CEF 全等时,求点 F 的速度和运动时间.

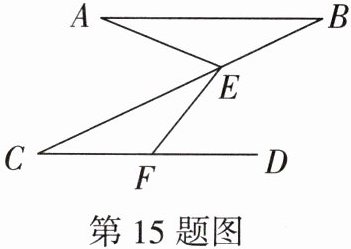
答案：
解:根据题意,得BE=4t,CE=BC−BE=16−4t,
　设点F的速度为每秒x个单位长度，则CF=xt,
∵AB//CD,
∴∠B=∠C,
　分情况讨论,如解图①,当△ABE≌△ECF时,
　AB=EC,BE=CF,
∴12=16−4t,4t=xt,
　解得t=1,x=4;
　如解图②,当△ABE≌△FCE时,AB=FC,
　BE=CE,
∴12=xt,4t=16−4t,
　解得t=2,x=6.
　综上所述,当△ABE和△CEF全等时,点F以每秒4个单位长度的速度运动1秒，或以每秒6个单位长度的速度运动2秒