《2025年万唯中考情境题八年级数学上册苏科版》

1. 下列函数中是正比例函数的是 (A)
A.$y = - 2x$
B.$y = \frac{1}{2x}$
C.$y = 5 - 0.2x$
D.$y = 2x^{2}$

答案： A

2. 下列函数中,$y是x$的一次函数的是 (B)
A.$y = 3x^{2}$
B.$y = - 4x - 1$
C.$y = \sqrt{x}$
D.$y = x^{3}$

答案： B

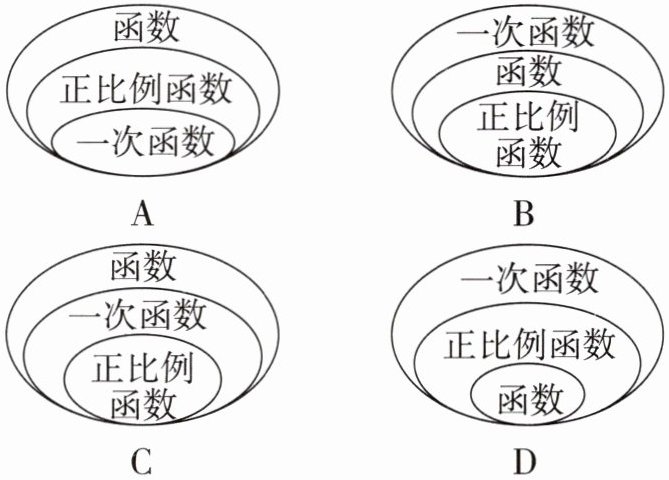
3. 下列选项中,表示函数、一次函数与正比例函数之间的关系的是 (C)
]

答案： C

4. 下列变量之间：①圆的面积$S与半径r$；②等边三角形的周长$C与边长a$；③正方体的体积$V与棱长x$；④等腰三角形顶角$\angle A与底角\angle B$,其中两个变量不满足正比例函数关系的是①③④(填序号)。

答案： ①③④

5. 已知函数$y = (3 - a)x + a^{2} - 9$。
(1)若此函数为一次函数,求$a$的取值范围；
(2)若此函数为正比例函数,求$a$的值。

答案： 解:
(1)若此函数为一次函数,则3-a≠0,解得a≠3,
∴该函数为一次函数时,a的取值范围为a≠3;
(2)若此函数为正比例函数,则3-a≠0,且a²-9=0,解得a=-3,
∴当a=-3时,该函数为正比例函数.

6. 幸福小区计划购进一批树苗绿化小区,已知一棵树苗15元,送货上门需要加100元运费,则所需总金额$y$(元)与购买棵树$x$(棵)之间的函数表达式为 (C)
A.$y = 15x$
B.$y = 100 - 15x$
C.$y = 15x + 100$
D.$y = 115x$

答案： C

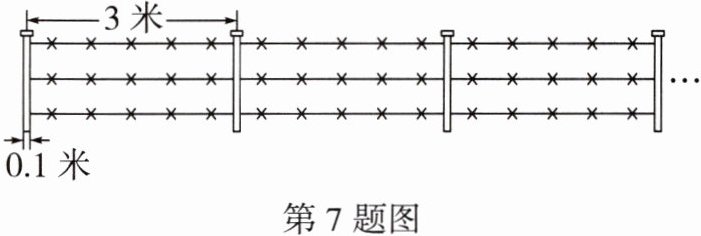
7. 小区绿化区安装的护栏示意图如图所示,每根立柱宽0.1米,立柱间距为3米。每根立柱的价格为30元。设立柱根数为$x$根,则护栏的总长度为$y$(米)与$x$(根)之间的函数表达式y=3.1x-3；购买立柱的费用$W$(元)与$x$(根)之间的函数表达式为W=30x。

答案： y=3.1x-3;W=30x

8. 小可家有一个水龙头坏了,无法拧紧,导致一直在滴水,为了避免浪费水,小可在这个水龙头下放了一个容量为250毫升的量杯(量杯中原15毫升的水),观察发现,量杯中的水平均每分钟增加5毫升,且量杯中现有的水量$y$(毫升)与放在水龙头下的时间$x$(分钟)之间的关系式为$y = kx + b(k \neq 0)$。
(1)求$k$,$b的值及x$的取值范围；
(2)请说明$k与b$的实际意义。

答案： 解:
(1)根据题意可知,这个水龙头平均1分钟能滴水5毫升,
∴量杯放在水龙头下x分钟后,量杯中的水增加5x毫升,量杯中现有的水量y(毫升)与放在水龙头下的时间x(分钟)之间的关系式为y=5x+15,
∴k=5,b=15,又
∵量杯的容量为250毫升,(250-15)÷5=47(分钟),
∴x的取值范围是0≤x≤47;
(2)k表示的实际意义是:这个水龙头滴水的速度是5毫升/分钟;b表示的实际意义是:量杯中原有的水量为15毫升.