第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. “6的算术平方根”用数学符号表示为 (
A.$\pm \sqrt{6}$
B.$\sqrt{6}$
C.$\pm \sqrt{3}$
D.$\sqrt{3}$
B
)A.$\pm \sqrt{6}$
B.$\sqrt{6}$
C.$\pm \sqrt{3}$
D.$\sqrt{3}$
答案:
B
2. $\sqrt{16}$的算术平方根是 (
A.4
B.$\pm 4$
C.2
D.$\pm 2$
C
)A.4
B.$\pm 4$
C.2
D.$\pm 2$
答案:
C 【解析】
∵√16=4,
∴4的算术平方根是2.
∵√16=4,
∴4的算术平方根是2.
3. 计算:$\sqrt{25}=$
5
;$-\sqrt{\frac{9}{4}}=$-3/2
.
答案:
5;-3/2
4. 若$\sqrt{x}= 3$,则x的值为
9
.
答案:
9
5. (教材练习第2题改编)计算:
(1)$\sqrt{3^{2}}=$
(2)$\sqrt{7^{2}}=$
(1)$\sqrt{3^{2}}=$
3
;$\sqrt{(-6)^{2}}=$6
;(2)$\sqrt{7^{2}}=$
7
;$(\sqrt{0.04})^{2}=$0.04
.
答案:
(1)3;6;
(2)7;0.04.
(1)3;6;
(2)7;0.04.
6. (教材例1改编)求出下列各数的算术平方根:
(1)36; (2)$\frac{169}{49}$; (3)$(-9)^{2}$;
(4)0.16; (5)$3 \frac{1}{16}$; (6)$10^{4}$.
(1)36; (2)$\frac{169}{49}$; (3)$(-9)^{2}$;
(4)0.16; (5)$3 \frac{1}{16}$; (6)$10^{4}$.
答案:
解:
(1)36的算术平方根是√36=6;
(2)169/49的算术平方根是√(169/49)=13/7;
(3)(-9)²的算术平方根是√(-9)²=√81=9;
(4)0.16的算术平方根是√0.16=0.4;
(5)3 1/16的算术平方根是√(3 1/16)=√(49/16)=7/4;
(6)10⁴的算术平方根是√10⁴=100.
(1)36的算术平方根是√36=6;
(2)169/49的算术平方根是√(169/49)=13/7;
(3)(-9)²的算术平方根是√(-9)²=√81=9;
(4)0.16的算术平方根是√0.16=0.4;
(5)3 1/16的算术平方根是√(3 1/16)=√(49/16)=7/4;
(6)10⁴的算术平方根是√10⁴=100.
7. 下列各数中没有算术平方根的是 (
A.-5
B.0
C.6
D.$|-3|$
A
)A.-5
B.0
C.6
D.$|-3|$
答案:
A 【解析】负数没有算术平方根,A选项符合题意;0的算术平方根是0,6>0,|-3|=3>0,B,C,D选项不符合题意.
8. 已知$|5+a|+\sqrt{b-3}= 0$,则a+b的值为______
-2
.
答案:
-2 【解析】
∵|5+a|≥0,√(b-3)≥0,|5+a|+√(b-3)=0,
∴|5+a|=0,√(b-3)=0,解得a=-5,b=3,则a+b=-5+3=-2.
∵|5+a|≥0,√(b-3)≥0,|5+a|+√(b-3)=0,
∴|5+a|=0,√(b-3)=0,解得a=-5,b=3,则a+b=-5+3=-2.
9. 已知a,b都是有理数,且$b= \sqrt{a-3}-\sqrt{9-3 a}+1$,求2a+b的值.
答案:
解:由题意得,a-3≥0,9-3a≥0,解得a=3,
∴a-3=0,9-3a=0.
∴b=0-0+1=1.
∴2a+b=2×3+1=7.
∴a-3=0,9-3a=0.
∴b=0-0+1=1.
∴2a+b=2×3+1=7.
10. 已知一种枪管长度s= 0.81m,子弹射出枪口时的速度$v= \sqrt{2 a s}$,其中$a= 5 × 10^{5} \mathrm{~m} / \mathrm{s}^{2}$,则v的值为 (
A.500m/s
B.600m/s
C.800m/s
D.900m/s
D
)A.500m/s
B.600m/s
C.800m/s
D.900m/s
答案:
D 【解析】v=√(2as)=√(2×5×10⁵×0.81)=900(m/s).
11. (教材习题第4题改编) 一题多变
变式1 改为求周长的倍数
如果一个正方形的面积扩大为原来9倍,那么它的周长变为原来的 (
A. 3倍 B. 6倍 C. 9倍 D. 12倍
变式2 改为正方形折叠
如图,将一张面积为$40cm^2$的正方形纸片折叠两次后仍为正方形,折叠后的正方形的边长为
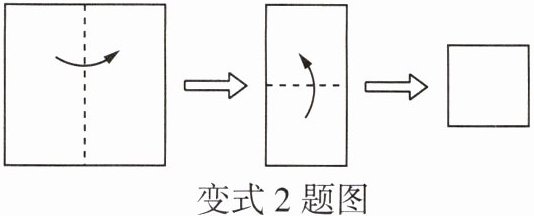
变式3 改为结合长方形比较边长大小
某校八年级学生制作了面积为$81cm^2$的正方形明信片.
(1)该明信片的边长为
(2)如图,已知信封的长是宽的2倍,面积为$242cm^2,$请问能否在不折叠的情况下将明信片放入此信封? 并说明理由.

变式1 改为求周长的倍数
如果一个正方形的面积扩大为原来9倍,那么它的周长变为原来的 (
A
)A. 3倍 B. 6倍 C. 9倍 D. 12倍
变式2 改为正方形折叠
如图,将一张面积为$40cm^2$的正方形纸片折叠两次后仍为正方形,折叠后的正方形的边长为
√10
cm.
变式3 改为结合长方形比较边长大小
某校八年级学生制作了面积为$81cm^2$的正方形明信片.
(1)该明信片的边长为
9
cm;(2)如图,已知信封的长是宽的2倍,面积为$242cm^2,$请问能否在不折叠的情况下将明信片放入此信封? 并说明理由.

能在不折叠的情况下能将明信片放入此信封.理由如下:设长方形信封的长为2x cm,则宽为x cm,由题意得2x·x=242,∴x²=121.∴x=√121=11,∴长方形的信封长为2×11=22(cm),由(1)可知明信片的边长是9 cm.∵9<11<22,∴能在不折叠的情况下将明信片放入此信封.
答案:
变式1 A 【解析】设原来正方形的边长为a,则周长为4a,面积为a²,
∴正方形的面积扩大为原来的9倍后的面积为9a²,
∴新正方形的边长为√(9a²)=3a,
∴新正方形的周长为12a,
∴它的周长变为原来的3倍.变式2 √10 【解析】根据题意可得折叠后正方形的面积为40÷4=10(cm²),
∴折叠后正方形的边长为√10cm.变式3 解:
(1)9;【解法提示】该明信片的边长为√81=9(cm).
(2)能在不折叠的情况下能将明信片放入此信封.理由如下:设长方形信封的长为2x cm,则宽为x cm,由题意得2x·x=242,
∴x²=121.
∴x=√121=11,
∴长方形的信封长为2×11=22(cm),由
(1)可知明信片的边长是9 cm.
∵9<11<22,
∴能在不折叠的情况下将明信片放入此信封.
∴正方形的面积扩大为原来的9倍后的面积为9a²,
∴新正方形的边长为√(9a²)=3a,
∴新正方形的周长为12a,
∴它的周长变为原来的3倍.变式2 √10 【解析】根据题意可得折叠后正方形的面积为40÷4=10(cm²),
∴折叠后正方形的边长为√10cm.变式3 解:
(1)9;【解法提示】该明信片的边长为√81=9(cm).
(2)能在不折叠的情况下能将明信片放入此信封.理由如下:设长方形信封的长为2x cm,则宽为x cm,由题意得2x·x=242,
∴x²=121.
∴x=√121=11,
∴长方形的信封长为2×11=22(cm),由
(1)可知明信片的边长是9 cm.
∵9<11<22,
∴能在不折叠的情况下将明信片放入此信封.
查看更多完整答案,请扫码查看


