《2025年万唯中考情境题八年级数学上册苏科版》

9. (教材P73第7题改编)如图,在△ABC中,AB= AC,AD平分∠BAC,交BC于点D,E是AB的中点,连接DE,若△ABC的面积为8,则四边形ACDE的面积为(B)
A.4
B.6
C.8
D.10

答案： B

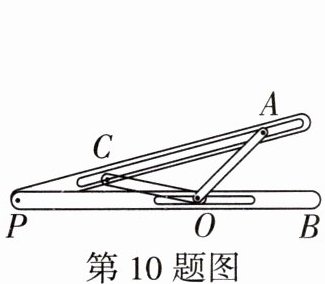
10. 数学文化情境 三等分角 如图,“三等分角器”是由两根有槽的棒PA,PB组成,两根棒在P点相连,并可绕点P转动,C点固定,O,A可在槽内滑动,OA= OC= PC,若∠AOB= 45°,则∠P的度数为15°。

答案： 15°

11. 如图,在Rt△ABC中,∠C= 90°,∠A= 30°,点D是AB的中点,点P是边AC上一动点,连接DP,将△ABC沿DP折叠,点A的对应点为点F,DF与AC相交于点E(点E不与点C重合)。若△ADE是以AE为腰的等腰三角形,则∠DEC的度数为______60°或105°。

答案： 60°或105°

12. (综合与实践·操作探究)如图,在数学课上,某同学用小棒进行如下探究：已知∠BAC= θ(0°＜θ＜90°)。从点$A_1$开始,用等长的小棒依次向右摆放在两射线之间,并使小棒两端分别落在射线AB,AC上,其中$A_1A_2,$为第1根小棒,且$A_1A_2= AA_1。$
(1)若$A_1A_2⊥A_2A_3,$则θ= ______22.5°；
(2)若已经摆放了3根小棒,求$θ_3$的值(用含θ的式子表示)；
解:∵A₁A₂=AA₁,∴∠A₁A₂A=∠AA₂A₁=θ,∴∠A₂A₁A₃=θ₁=θ+θ,∴θ₁=2θ,同理可得θ₂=∠AA₄A₃=3θ,∴θ₃=4θ;
(3)若正好摆放5根小棒,求θ的最小值。
解:由题意得,当第5根小棒正好与射线垂直时,θ的值最小,∵θ₅=6θ,∴6θ=90°,解得θ=15°,即θ的最小值为15°.

答案： 解:
(1)22.5°;
(2)
∵A₁A₂=AA₁,
∴∠A₁A₂A=∠AA₂A₁=θ,
∴∠A₂A₁A₃=θ₁=θ+θ,
∴θ₁=2θ,同理可得θ₂=∠AA₄A₃=3θ,
∴θ₃=4θ;
(3)由题意得,当第5根小棒正好与射线垂直时,θ的值最小,
∵θ₅=6θ,
∴6θ=90°,解得θ=15°,即θ的最小值为15°.

1. 如图,在△ABC中,AB= AC= 5,BC= 6,点E为BC中点,过点E作EF⊥AC于点F,若S_{△ABC}= 12,则EF的长为$\frac{12}{5}$。

答案： $\frac{12}{5}$

2. 如图,在△ABC中,AB= AC,作△ACD,使得AC= CD。H为AD的中点,连接CH,且CH= 5,若∠BAC+∠ACD= 180°,则BC的长为______10。

答案： 10