第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
10. (教材习题第1题改编) 一题多变
变式1 列表求未知数的值
已知一次函数$y = kx + b(k \neq 0)$,下表列出了$x和y$的部分对应值,则$a^{2024}$的值为 (


A.0
B.1
C.-1
D.2024
变式2 根据程序框图求函数值
根据如图所示的程序,当输入值为-1,2时,输出$y$的值分别为-13,11,若输入$x$的值为3,则输出$y$的值为
变式1 列表求未知数的值
已知一次函数$y = kx + b(k \neq 0)$,下表列出了$x和y$的部分对应值,则$a^{2024}$的值为 (
B
)

A.0
B.1
C.-1
D.2024
变式2 根据程序框图求函数值
根据如图所示的程序,当输入值为-1,2时,输出$y$的值分别为-13,11,若输入$x$的值为3,则输出$y$的值为
14
.
答案:
10. 变式1 B 变式2 14
11. 跨学科情境 物理声音传播速度 经研究发现,声音在空气中的传播速度$v(\text{m/s})与空气的温度T(^{\circ}\text{C})$之间在一定范围内存在一次函数关系,如下表所示:
|$T(^{\circ}\text{C})$|-20|-10|0|10|20|30|
|$v(\text{m/s})$|318|324|330|336|342|348|

(1)写出当$-20 \leq T \leq 30$时,$v与T$之间的函数表达式;
(2)气温在$22^{\circ}\text{C}$时,有人在看到闪电5 s后听到雷声,请通过计算估计此人距打雷处的距离(人看到闪电的时间忽略不计).
|$T(^{\circ}\text{C})$|-20|-10|0|10|20|30|
|$v(\text{m/s})$|318|324|330|336|342|348|

(1)写出当$-20 \leq T \leq 30$时,$v与T$之间的函数表达式;
(2)气温在$22^{\circ}\text{C}$时,有人在看到闪电5 s后听到雷声,请通过计算估计此人距打雷处的距离(人看到闪电的时间忽略不计).
答案:
解:
(1)设 v 与 T 之间的函数表达式为$v=kT+b(k≠0)$,将$T=0,v=330$和$T=10,v=336$代入$v=kT+b$,得$\begin{cases}b=330,\\10k+b=336,\end{cases}$解得$\begin{cases}b=330,\\k=0.6,\end{cases}$
∴ 当$-20\leqslant T\leqslant30$时,v 与 T 之间的函数表达式为$v=0.6T+330$;
(2)当$T=22$时,$v=0.6×22+330=343.2$,由题意得$343.2×5=1716(m)$.答:此人距打雷处的距离约为 1716 m.
(1)设 v 与 T 之间的函数表达式为$v=kT+b(k≠0)$,将$T=0,v=330$和$T=10,v=336$代入$v=kT+b$,得$\begin{cases}b=330,\\10k+b=336,\end{cases}$解得$\begin{cases}b=330,\\k=0.6,\end{cases}$
∴ 当$-20\leqslant T\leqslant30$时,v 与 T 之间的函数表达式为$v=0.6T+330$;
(2)当$T=22$时,$v=0.6×22+330=343.2$,由题意得$343.2×5=1716(m)$.答:此人距打雷处的距离约为 1716 m.
12. (项目式学习·探究龟兔赛跑)阅读下面材料,回答下列问题.
【问题情境】
在龟兔赛跑游戏中,已知跑道长100 m,二者同时从起点出发,兔子速度快,但由于中途休息并睡着,导致乌龟比兔子先到达终点.
【问题解决】
任务一:已知在比赛中乌龟匀速爬行,在125 min后到达终点,则乌龟爬行的路程$s(m)与所用时间t(min)$之间的函数表达式为
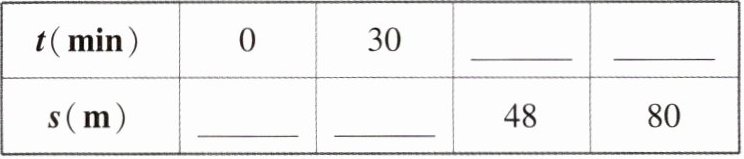
任务二:①结合任务一的函数表达式,完成下面乌龟爬行时间$t(min)与其爬行路程s(m)$的表格;
②若乌龟距离终点还有10 m时,兔子醒来并以8 m/min的速度跑去终点,此时兔子距离终点90 m,试判断兔子能否比乌龟先到终点,并说明理由.
【问题情境】
在龟兔赛跑游戏中,已知跑道长100 m,二者同时从起点出发,兔子速度快,但由于中途休息并睡着,导致乌龟比兔子先到达终点.
【问题解决】
任务一:已知在比赛中乌龟匀速爬行,在125 min后到达终点,则乌龟爬行的路程$s(m)与所用时间t(min)$之间的函数表达式为
$s=0.8t(0\leqslant t\leqslant125)$
;任务二:①结合任务一的函数表达式,完成下面乌龟爬行时间$t(min)与其爬行路程s(m)$的表格;

②若乌龟距离终点还有10 m时,兔子醒来并以8 m/min的速度跑去终点,此时兔子距离终点90 m,试判断兔子能否比乌龟先到终点,并说明理由.
任务一:$s=0.8t(0\leqslant t\leqslant125)$;任务二:①从左到右,依次填入 0,24,60,100;②兔子能比乌龟先到达终点.理由如下:乌龟最后 10 m 所用时间为$t_{1}=\frac{10}{0.8}=12.5(min)$,而兔子最后 90 m 所用时间为$t_{2}=\frac{90}{8}=11.25(min)$,$\because12.5>11.25$,即$t_{1}>t_{2}$,∴ 兔子能比乌龟先到达终点.
答案:
解:任务一:$s=0.8t(0\leqslant t\leqslant125)$;任务二:①从左到右,依次填入 0,24,60,100;②兔子能比乌龟先到达终点.理由如下:乌龟最后 10 m 所用时间为$t_{1}=\frac{10}{0.8}=12.5(min)$,而兔子最后 90 m 所用时间为$t_{2}=\frac{90}{8}=11.25(min)$,$\because12.5>11.25$,即$t_{1}>t_{2}$,
∴ 兔子能比乌龟先到达终点.
∴ 兔子能比乌龟先到达终点.
查看更多完整答案,请扫码查看


