第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 在$\triangle ABC$中,下列条件能判定$\triangle ABC$是等腰三角形的是(
A.$∠A = 60^{\circ},∠B = 100^{\circ}$
B.$∠A = 50^{\circ},∠B = 100^{\circ}$
C.$∠A = 40^{\circ},∠B = 100^{\circ}$
D.$∠A = 30^{\circ},∠B = 100^{\circ}$
C
)A.$∠A = 60^{\circ},∠B = 100^{\circ}$
B.$∠A = 50^{\circ},∠B = 100^{\circ}$
C.$∠A = 40^{\circ},∠B = 100^{\circ}$
D.$∠A = 30^{\circ},∠B = 100^{\circ}$
答案:
C
2. 日常生活情境 平板保护壳 如图是一个自带支架的平板保护壳及其简易图,若$∠ACB = ∠ABC,AB = 12cm$,则AC的长为
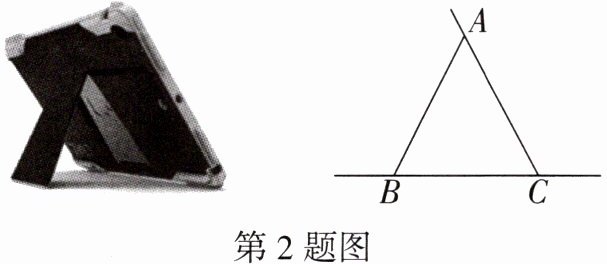
12
cm.
答案:
12
3. (教材习题第5题改编) 一题多变
变式1 变为计算线段长
如图,已知线段AC,BD相交于点O,$AB// DC,OA = OB$,若$OC = 3$,则OD的长为
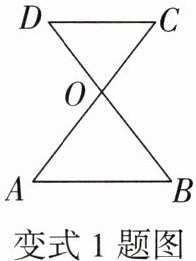

变式2 改变平行线的位置
如图,在$\triangle ABC$中,D是AC边上的中点,$AE// BC$,连接DE,已知$∠B = ∠C = ∠E$,若$AB = 8$,则DE的长为
变式1 变为计算线段长
如图,已知线段AC,BD相交于点O,$AB// DC,OA = OB$,若$OC = 3$,则OD的长为
3
.

变式2 改变平行线的位置
如图,在$\triangle ABC$中,D是AC边上的中点,$AE// BC$,连接DE,已知$∠B = ∠C = ∠E$,若$AB = 8$,则DE的长为
4
.
答案:
变式1 3 变式2 4
4. (教材练习第1题改编)如图,一艘船从点A出发,沿正东方向行驶,在点A处测得灯塔C在北偏东$58^{\circ}$方向上,船行驶50海里到达B处,此时测得灯塔C在北偏东$26^{\circ}$方向上,则BC之间的距离为
50
海里.
答案:
50
5. (教材练习第1题改编)如图,在$\triangle ABC$中,D是BC边上的点,连接AD. 若$∠C = ∠B,∠ADC = 2∠B,∠BAC = 3∠B$,则图中的等腰三角形有
3
个.
答案:
3
6. 如图,在$\triangle ABC$中,D,E是边BC的三等分点,连接AD,AE,$∠ADE = ∠AED = 36^{\circ}$,找出图中所有的等腰三角形并证明.
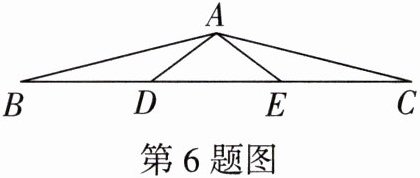

答案:
解:△ADE和△ABC是等腰三角形. 证明如下:
∵∠ADE=∠AED=36°,
∴AD=AE,∠ADB=∠AEC,
∴△ADE是等腰三角形;
∵D,E是边BC的三等分点,
∴BD=DE=CE.
在△ADB和△AEC中,$\left\{\begin{array}{l} AD=AE,\\ ∠ADB=∠AEC,\\ BD=CE,\end{array}\right. $
∴△ADB≌△AEC(SAS),
∴AB=AC,
∴△ABC是等腰三角形.
∵∠ADE=∠AED=36°,
∴AD=AE,∠ADB=∠AEC,
∴△ADE是等腰三角形;
∵D,E是边BC的三等分点,
∴BD=DE=CE.
在△ADB和△AEC中,$\left\{\begin{array}{l} AD=AE,\\ ∠ADB=∠AEC,\\ BD=CE,\end{array}\right. $
∴△ADB≌△AEC(SAS),
∴AB=AC,
∴△ABC是等腰三角形.
7. (教材习题第2题改编)如图,在$\triangle ABC$中,D,E分别是边AC,AB上的点,连接DE并延长至点F,连接BF,使得$∠ABF = ∠A$. 已知$DE// BC,AC = BC$,求证:$\triangle BEF$是等腰三角形.


答案:
证明:
∵DE//BC,
∴∠ABC=∠BEF,
∵AC=BC,
∴∠ABC=∠A,
∴∠BEF=∠A,
又
∵∠ABF=∠A,
∴∠ABF=∠BEF,
∴BF=EF,即△BEF是等腰三角形.
∵DE//BC,
∴∠ABC=∠BEF,
∵AC=BC,
∴∠ABC=∠A,
∴∠BEF=∠A,
又
∵∠ABF=∠A,
∴∠ABF=∠BEF,
∴BF=EF,即△BEF是等腰三角形.
查看更多完整答案,请扫码查看


