第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
7. 如图,在△ABC和△BDE中,点D在线段BC上,DE与AB交于点F. 若BC= DE,AC= BE,AB= BD,∠ABC= 50°,则∠BFD的度数为 (
A.50°
B.60°
C.70°
D.80°
D
)A.50°
B.60°
C.70°
D.80°
答案:
D
8. 如图是由六根木条钉成的木架,要使该木架稳固且不变形,则至少需要再钉上木条的根数为 (
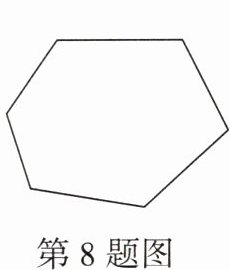
A.1
B.2
C.3
D.4
C
) 
A.1
B.2
C.3
D.4
答案:
C
9. (中考新考法·注重学习过程) 如图,在△ABC中,AB= AC,求证:∠B= ∠C,小珍的证明过程如下:
证明:在△ABC和△ACB中,
$\begin{cases} BC= CB, \\ AC= AB, \\ AB= AC, \end{cases} $
∴△ABC≌△ACB(SSS).
∴∠B= ∠C.

请问小珍的作法______
证明:在△ABC和△ACB中,
$\begin{cases} BC= CB, \\ AC= AB, \\ AB= AC, \end{cases} $
∴△ABC≌△ACB(SSS).
∴∠B= ∠C.

请问小珍的作法______
错误
(填“正确”或“错误”).
答案:
错误
10. (教材练习第3题改编) 如图,在正方形网格中,点A,B,C,D,E均在格点上,取一格点F使得△DEF与△ABC全等,则符合要求的点有

4
个.
答案:
解:在正方形网格中,先计算△ABC各边长度。设每个小正方形边长为1,根据勾股定理可得:AB=√[(1-0)²+(2-1)²]=√2,BC=√[(2-1)²+(1-0)²]=√2,AC=√[(2-0)²+(1-2)²]=√5。
要使△DEF与△ABC全等,则△DEF的三边也应为√2,√2,√5。已知D、E两点位置,DE=2(横向两个单位长度)。
分情况讨论:
1. 当DE对应AB(或BC)时,在DE上方和下方分别寻找点F,使DF=√2,EF=√5或DF=√5,EF=√2,可找到2个点。
2. 当DE对应AC时,在DE上方和下方分别寻找点F,使DF=√2,EF=√2,可找到2个点。
综上,符合要求的点F共有4个。
答案:4
要使△DEF与△ABC全等,则△DEF的三边也应为√2,√2,√5。已知D、E两点位置,DE=2(横向两个单位长度)。
分情况讨论:
1. 当DE对应AB(或BC)时,在DE上方和下方分别寻找点F,使DF=√2,EF=√5或DF=√5,EF=√2,可找到2个点。
2. 当DE对应AC时,在DE上方和下方分别寻找点F,使DF=√2,EF=√2,可找到2个点。
综上,符合要求的点F共有4个。
答案:4
11. (教材复习题第10题改编) 如图,在△ABC中,∠ABC= 90°,D,E分别为边AC,BC上一点,连接BD,DE. 已知AB= BE,AD= DE.
(1) 求证:BD平分∠ABC;
(2) 若∠CDE= 20°,求∠A的度数.
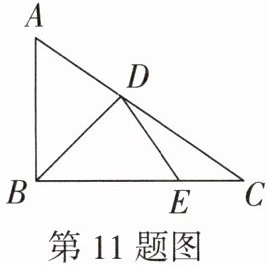
(1) 求证:BD平分∠ABC;
(2) 若∠CDE= 20°,求∠A的度数.

答案:
∴∠ADB=∠EDB= $\frac{1}{2}(180^{\circ}-\angle CDE)=80^{\circ}$,
∴∠A=180°-∠ABD-∠ADB=55°.
∴∠ADB=∠EDB= $\frac{1}{2}(180^{\circ}-\angle CDE)=80^{\circ}$,
∴∠A=180°-∠ABD-∠ADB=55°.
1. 如图,AD与BC相交于点O,已知AB= CD,AD= BC,若∠B= 15°,∠AOB= 95°,则∠C的度数为
70°
.
答案:
70°
2. 如图,四边形ABCD与四边形GBEF是两个完全相等,且边长均为4的正方形,将它们叠起,使得点M恰好是AD和EF的中点,则阴影部分的面积为
8
.
答案:
8
查看更多完整答案,请扫码查看


