第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 下列图形中具有稳定性的是 (

B
)
答案:
B
2. 如图,老师讲桌上的一个三角形卡片被压在了书下,请你根据三角形卡片露出的部分判断该三角形的形状是 (
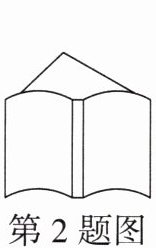
A.等边三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
D
)
A.等边三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
答案:
D
3. 如图,$AB// CD$,$EF交AB于点G$,连接$AE$,$∠A= 32^{\circ}$,$∠E= 90^{\circ}$,则$∠EFD$的度数为 (
A.$120^{\circ}$
B.$122^{\circ}$
C.$125^{\circ}$
D.$130^{\circ}$
B
)A.$120^{\circ}$
B.$122^{\circ}$
C.$125^{\circ}$
D.$130^{\circ}$
答案:
B
4. 如图,将$△ABC沿BC所在直线翻折得到△DBC$,则下列说法中不正确的是 (
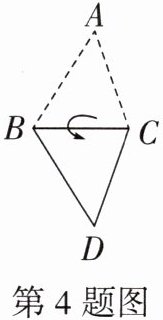
A.$△BDC\cong △BAC$
B.$AB= DB$
C.$AB// CD$
D.$CB平分∠ACD$
C
)
A.$△BDC\cong △BAC$
B.$AB= DB$
C.$AB// CD$
D.$CB平分∠ACD$
答案:
C
5. 如图,已知$AB// CF$,$D是AB$上一点,$DF交AC于点E$,若$AB= BD+CF$,$AC= 10$,则$AE$的长为 (
A.4
B.5
C.8
D.10
B
)A.4
B.5
C.8
D.10
答案:
B
6. 如图,$△ABC和△ADE$均为等腰直角三角形,连接$CD$,且点$C$,$D$,$E$在同一条直线上,连接$BD$,$BE$,则以下四个结论:①$BD= CE$;②$∠ACE+∠DBC= 45^{\circ}$;③$BD⊥CE$;④$∠BAE+∠DAC= 180^{\circ}$.其中正确的结论有 (
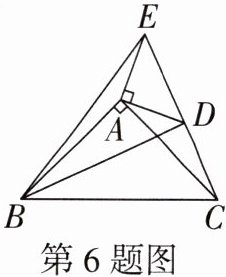
A.①②③
B.①②④
C.②③④
D.①②③④
D
)
A.①②③
B.①②④
C.②③④
D.①②③④
答案:
D
7. 如图,已知$AB// CD$,欲证明$△ABC\cong △CDA$,需补充条件是
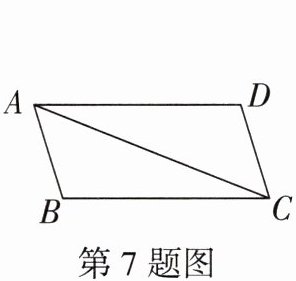
AB=CD(答案不唯一)
(写出一个即可).
答案:
AB=CD(答案不唯一)
8. 如图,$AD$,$CE是△ABC$的高,若$AB= 9$,$AD= 6$,$CE= 2$,则$BC$的长为
3
.
答案:
3
9. 如图,在$△ABC和△BDE$中,点$A$,$B$,$E$共线,点$B$,$C$,$D$共线,$BF$,$BG分别是∠ABD和∠DBE$的平分线,已知$∠ABD= ∠DBE$,$AB= DB$,$EB= CB$,若$BF= 2$,则$BG$的长为____
2
.
答案:
2
10. 如图,在四边形$ABCD$中,$AB= BC= 8cm$,$CD= 6cm$,$∠B= ∠C$,动点$P$,$Q分别从A$,$B$两点同时出发,沿$AB$,$BC$方向匀速运动,连接$PQ$,$DQ$,点$P的运动速度为1cm/s$,点$Q的运动速度为2cm/s$,当点$Q到达点C$时,$P$,$Q$两点都停止运动.若运动过程中某一时刻以$B$,$P$,$Q为顶点的三角形与以D$,$Q$,$C$为顶点的三角形全等,则运动时间为
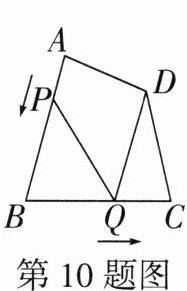
2
s.
答案:
2
11. 已知$△ABC的三边a$,$b$,$c满足a+b= 3c-4$,$a-b= 2c-6$,且$a>b$.
(1)求$c$的取值范围;
(2)若$△ABC的周长为12$,求$c$的值.
(1)求$c$的取值范围;
(2)若$△ABC的周长为12$,求$c$的值.
答案:
11. 解:
(1)
∵a+b=3c - 4,a - b=2c - 6,a,b,c分别为△ABC的三边,
∴a+b>c,a - b<c,
∴{3c - 4>c,2c - 6<c,解得2<c<6,
∴c的取值范围为2<c<6;
(2)
∵△ABC的周长为12,a+b=3c - 4,
∴a+b+c=4c - 4=12,解得c=4,
∴c的值是4.
(1)
∵a+b=3c - 4,a - b=2c - 6,a,b,c分别为△ABC的三边,
∴a+b>c,a - b<c,
∴{3c - 4>c,2c - 6<c,解得2<c<6,
∴c的取值范围为2<c<6;
(2)
∵△ABC的周长为12,a+b=3c - 4,
∴a+b+c=4c - 4=12,解得c=4,
∴c的值是4.
查看更多完整答案,请扫码查看


