《2025年万唯中考情境题八年级数学上册苏科版》

10. (教材复习题第7题改编)如图,将一个等边△ABC纸片沿BC向右平移2cm后得到△DEF,若AB= 6cm,则两个三角形重叠部分的周长为(C)
A.6cm
B.9cm
C.12cm
D.15cm

答案： C

11. 如图,小琼将长方形纸片ABCD对折后展开,折痕为EF,H为CD边上一点,再将△BCH沿BH翻折,点C恰好落在EF边上的点G处,则∠BHC的度数为(D)
A.30°
B.40°
C.50°
D.60°

答案： D

12. 如图是一副叠放在一起的三角板,若AC= 24,则阴影部分的面积为______72.

答案： 72

选择的条件：①③；
证明的结论：②
证明如下：
∵ BE=ED，∠E=60°，
∴ △EBD是等边三角形，
∴ ∠EBD=60°.
∵ AB⊥ED，即∠BAD=90°，AB是ED边上的高，
∴ BA平分∠EBD，
∴ ∠ABD=1/2∠EBD=30°.
∵ AB=AC，
∴ ∠C=∠ABD=30°，
∴ ∠BAC=180°-∠C-∠ABD=180°-30°-30°=120°，
∴ ∠DAC=∠BAC-∠BAD=120°-90°=30°，
∴ ∠C=∠DAC，
∴ AD=CD

答案： 解:①③;②.证明:
∵ BE=ED,∠E=60°.
∴ △EBD 是等边三角形,
∴ ∠EBD=60°.又
∵ AB⊥ED,即∠BAD=90°,AB 是 ED 边上的高,
∴ BA 平分∠EBD,
∴ ∠ABD=1/2∠EBD=30°.又
∵ AB=AC,
∴ ∠C=∠ABD=30°,
∴ ∠BAC=180°-∠C-∠ABD=180°-30°-30°=120°,
∴ ∠DAC=∠BAC-∠BAD=120°-90°=30°,
∴ ∠C=∠DAC,
∴ AD=CD(答案不唯一).

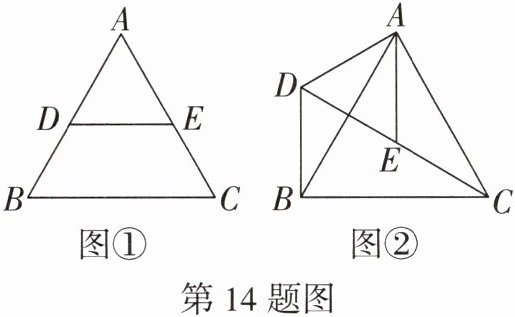
14. (中考新考法·教材素材拓展)已知△ABC为等边三角形.
(1)如图①,DE//BC,DE分别交AB,AC于点D,E. 求证：△ADE为等边三角形. 针对此题,课本给出了如下的证明方法：
证明：∵△ABC为等边三角形,
∴∠A= ∠B= ∠C= 60°(等边三角形的性质定理).
∵DE//BC,
∴∠ADE= ∠B= 60°,∠AED= ∠C= 60°.
∴∠A= ∠ADE= ∠AED.
∴△ADE是等边三角形(等边三角形的判定定理).
请你用另一种方法证明此题；
(2)如图②,△ABC,△ADE仍是等边三角形,连接CE,连接BD,求证：BD= CE.

答案： 证明:
(1)
∵ △ABC 为等边三角形,
∴ ∠B=∠C=∠A=60°,
∵ DE//BC,
∴ ∠ADE=∠B,∠AED=∠C,
∴ ∠ADE=∠AED,
∴ AD=AE,
∴ △ADE 为等腰三角形,又
∵ ∠A=60°,
∴ △ADE 是等边三角形;
(2)
∵ △ABC,△ADE 是等边三角形,
∴ AB=AC,AD=AE,∠DAE=∠BAC=60°,又
∵ ∠DAB=∠DAE-∠BAE,∠EAC=∠BAC-∠BAE,
∴ ∠DAB=∠EAC.在△DAB 和△EAC 中,{AD=AE,∠DAB=∠EAC,AB=AC,
∴ △DAB≌△EAC(SAS),
∴ BD=CE.