《2025年万唯中考情境题八年级数学上册苏科版》

1. 在$△ABC$中,$AB = 5$,$AC = 2$,$BC = a$,则$a$的值可以是(C)
A.2
B.3
C.5
D.7

答案： C

2. (黑白卷)从长度分别为3,4,8,10的四条线段中任意取三条,则取出的三条线段能组成三角形的情况有(B)
A.1种
B.2种
C.3种
D.4种

答案： B 【解析】根据三角形任意两边之和大于第三边，任意两边之差小于第三边可知，取出的三条线段能组成三角形的情况有：3,8,10 和 4,8,10 两种.

3. 日常生活情境 测量池塘 如图,为了估计一个池塘的宽度AB,小庆在岸上取一点P,经测量得$AP = 7m$,$BP = 3m$,则池塘宽度AB的取值范围为4 m＜AB＜10 m.

答案： 4 m＜AB＜10 m

4. (教材练习第1题改编)以下列长度的三条线段为边能否构成三角形？
①$3k$,$9k$,$5k(k ＞ 0)$；
②三条线段的长度之比为$2:2:3$；
③$x + 2$,$x + 3$,$x + 5(x ＞ 0)$。

答案： 解：根据三角形的三边关系，①
∵3k+5k＜9k，k＞0，
∴3k,9k,5k(k＞0)不能构成三角形；②
∵2+2＞3，2-2＜3，
∴三条线段的长度之比为2:2:3，可以构成三角形；③
∵x+2+x+3＞x+5，x+3-x-2＜x+5，x＞0，
∴x+2,x+3,x+5(x＞0)可以构成三角形.

5. (教材练习第2题改编)如图,在$△ABC$中,$DA⊥AC$于点A,交BC于点D,则$△ADC$的形状为直角(填“锐角”“直角”或“钝角”)三角形,其中钝角三角形为△ABC和△ABD.

答案： 直角，△ABC和△ABD

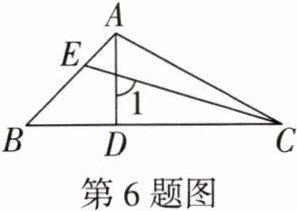
6. (教材习题第4题改编)如图,在$△ABC$中,$AD⊥BC$于点D,E是AB边上一点,连接CE,已知$BE ＜ CE$,则$∠BAD$＜$∠1$(填“＞”“＜”或“=”)。

答案： ＜

7. (教材练习第3题)如图,在$Rt△ABC$中,$∠ACB = 90^{\circ}$,在AB上取一点D,连接CD,使得$∠ADC = ∠ACD$,比较BD和BC的大小,并说明理由。

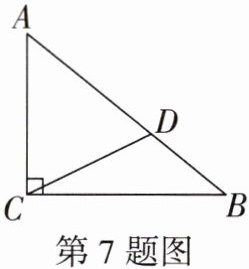
答案： 解：BD＜BC.理由如下：
∵∠ACB=90°，
∴∠ACD+∠BCD=90°，又
∵∠ADC+∠BDC=180°(平角定义)，且∠ADC=∠ACD，
∴∠BDC=180°-∠ADC=180°-∠ACD.
∵∠ACD+∠BCD=90°，
∴∠ACD=90°-∠BCD，则∠BDC=180°-(90°-∠BCD)=90°+∠BCD，
∴∠BDC＞∠BCD.根据“大角对大边”的性质，即在一个三角形中，大角所对的边较大.在△BCD中，
∵∠BDC＞∠BCD，
∴BD＜BC.

8. (综合与实践·图形变化探究)在学习完三角形的三边关系后,小可进一步利用三角形的三边关系探究线段的大小关系。
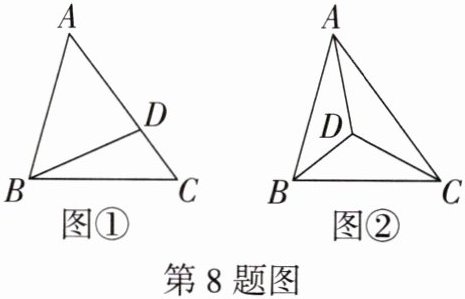
【探究一】如图①,在$△ABC$中,若点D在AC上,连接BD,$AD = BD$,则AC＞BC(填“＞”“＜”或“=”)；
【探究二】如图②,若D是$△ABC$内任意一点,试探究$\frac{1}{2}(AB + BC + AC)与AD + BD + CD$的大小关系。

解：【探究二】
∵在△ABD中，BD+AD＞AB，在△BCD中，BD+CD＞BC，在△ACD中，CD+AD＞AC，
∴BD+AD+BD+CD+CD+AD＞AB+BC+AC，即2(AD+BD+CD)＞AB+BC+AC，
∴$\frac{1}{2}(AB+BC+AC)$＜AD+BD+CD.

答案： 解：【探究一】＞；【探究二】
∵在△ABD中，BD+AD＞AB，在△BCD中，BD+CD＞BC，在△ACD中，CD+AD＞AC，
∴BD+AD+BD+CD+CD+AD＞AB+BC+AC，即2(AD+BD+CD)＞AB+BC+AC，
∴$\frac{1}{2}(AB+BC+AC)$＜AD+BD+CD.