第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 在△ABC中,AB= AC,∠B= 65°。则∠A的度数为(
A.50°
B.55°
C.60°
D.65°
A
)A.50°
B.55°
C.60°
D.65°
答案:
A
2. (教材练习第1题改编)如图,AB//CD。点E在线段AD上,AB= AE,连接BE,若∠ADC= 20°,则∠B的度数为
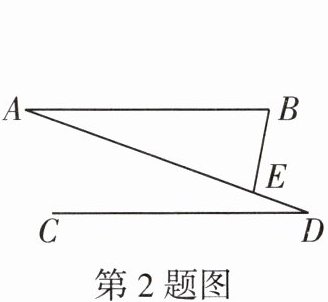
80°
。
答案:
80°
3. (黑白卷改编)如图,在△ABC中,AB= AC,D为AC上一点,连接BD,BD= BC。若∠C= 2∠A。则∠BDC的度数为

72°
。
答案:
72°
4. 一题多解法 如图,在△ABC中,AB= BC,AD,CE分别是BC,AB上的中线。求证:∠CAD= ∠ACE。


答案:
证明:证法一:
∵AB=BC,
∴∠BAC=∠ACB,
∵AD,CE分别是BC,AB上的中线,
∴AE=DC,在△ACE和△CAD中,$\left\{\begin{array}{l} AC=CA,\\ ∠EAC=∠DCA,\\ AE=CD,\end{array}\right. $
∴△ACE≌△CAD(SAS),
∴∠CAD=∠ACE.
∵AB=BC,
∴∠BAC=∠ACB,
∵AD,CE分别是BC,AB上的中线,
∴AE=DC,在△ACE和△CAD中,$\left\{\begin{array}{l} AC=CA,\\ ∠EAC=∠DCA,\\ AE=CD,\end{array}\right. $
∴△ACE≌△CAD(SAS),
∴∠CAD=∠ACE.
5. 传统文化情境 古建筑 如图①是我国古建筑梁架示意图,其顶部可看作一个等腰△ABC(如图②),已知AB= AC,则下列不能说明BD= CD的是(

A.AD⊥BC
B.∠BAD= ∠CAD
C.∠B= ∠C
D.△ABD≌△ACD
C
)
A.AD⊥BC
B.∠BAD= ∠CAD
C.∠B= ∠C
D.△ABD≌△ACD
答案:
C
6. (教材习题第2题改编)一题多变
变式1 改为已知高线求线段长
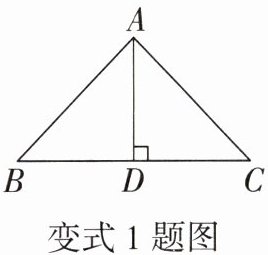
如图,在△ABC中,AB= AC,AD⊥BC于点D,若BC= 6,则CD的长为
变式2 改为已知中线求角度
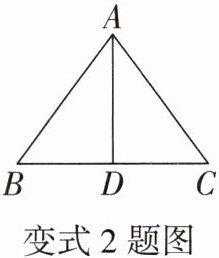
如图,在△ABC中,AB= AC,AD为△ABC的中线,若∠B= 50°,则∠DAC的度数是
变式1 改为已知高线求线段长
如图,在△ABC中,AB= AC,AD⊥BC于点D,若BC= 6,则CD的长为
3
。

变式2 改为已知中线求角度
如图,在△ABC中,AB= AC,AD为△ABC的中线,若∠B= 50°,则∠DAC的度数是
40°
。
答案:
变式1 3 变式2 40°
7. 一题多解法 如图,在△ABC中,AB= AC,D是三角形内一点,连接DA,DB,DC,且DB= DC。求证:AD⊥BC。


答案:
证明:证法一:在△ABD和△ACD中,$\left\{\begin{array}{l} AB=AC,\\ DB=DC,\\ AD=AD,\end{array}\right. $
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,又
∵AB=AC,
∴AD⊥BC.证法二:见详解
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,又
∵AB=AC,
∴AD⊥BC.证法二:见详解
8. 如图,作一个以AB为底边,底边上的高CD= AB的等腰三角形(保留作图痕迹,不写作法)。


答案:
解:作等腰△ABC如解图.
解:作等腰△ABC如解图.

查看更多完整答案,请扫码查看


