第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. (教材练习第2题改编) 一题多变
变式1 选择条件证明全等
如图,在△ABC和△DEF中,AB= DE,AC= DF,要利用“SSS”判定△ABC≌△DEF,则还需添加的条件为______
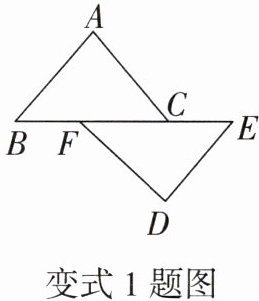
变式2 添加两条线段证明全等
如图,点B,D,C,F在同一条直线上,且AB= EF,BD= CF,AC= DE. 求证:△ABC≌△EFD.
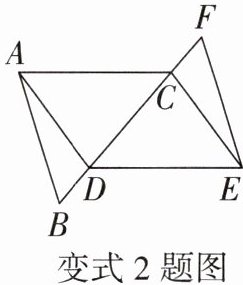
变式1 选择条件证明全等
如图,在△ABC和△DEF中,AB= DE,AC= DF,要利用“SSS”判定△ABC≌△DEF,则还需添加的条件为______
BC=EF
.
变式2 添加两条线段证明全等
如图,点B,D,C,F在同一条直线上,且AB= EF,BD= CF,AC= DE. 求证:△ABC≌△EFD.

证明:
$\because BD=CF$,
$\therefore BC=DF$,
在$\bigtriangleup ABC$和$\bigtriangleup EFD$中,
$\begin{cases}AB=EF,\\AC=DE,\\BC=DF.\end{cases}$
$\therefore \bigtriangleup ABC\cong\bigtriangleup EFD(SSS)$。
$\because BD=CF$,
$\therefore BC=DF$,
在$\bigtriangleup ABC$和$\bigtriangleup EFD$中,
$\begin{cases}AB=EF,\\AC=DE,\\BC=DF.\end{cases}$
$\therefore \bigtriangleup ABC\cong\bigtriangleup EFD(SSS)$。
答案:
变式1:$BC = EF$;
变式2:证明过程如上述解析。
变式2:证明过程如上述解析。
2. 如图,在四边形ABCD中,对角线AC,BD相交于点O. 已知AD= BC,AC= BD. 若∠ACD= 30°,则∠AOD的度数为 (
A.50°
B.60°
C.70°
D.80°
B
)A.50°
B.60°
C.70°
D.80°
答案:
B
3. (黑白卷改编) 如图,点A,D,C,F在同一条直线上,AD= CF,AB= DE,BC= EF,下列结论不一定正确的是 (
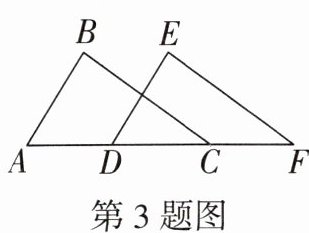
A.△ABC≌△DEF
B.∠B= ∠E
C.∠A= ∠F
D.BC//EF
C
)
A.△ABC≌△DEF
B.∠B= ∠E
C.∠A= ∠F
D.BC//EF
答案:
C
4. 日常生活情境 雨伞 如图是一把没有完全打开的伞的示意图,伞骨架AB= AC,支撑杆DE= DF,此时AE= $\frac{2}{3}$AB,AF= $\frac{2}{3}$AC. 在伞打开的过程中,AD始终平分∠BAC,请用所学数学知识说明其中的道理.


答案:
证明:
∵AB=AC,AE=$\frac{2}{3}$AB,AF=$\frac{2}{3}$AC,
∴AE=AF。
在△AED和△AFD中,
$\left\{\begin{array}{l}AE=AF\\AD=AD\\DE=DF\end{array}\right.$
∴△AED≌△AFD(SSS)。
∴∠EAD=∠FAD。
即AD平分∠BAC。
∵AB=AC,AE=$\frac{2}{3}$AB,AF=$\frac{2}{3}$AC,
∴AE=AF。
在△AED和△AFD中,
$\left\{\begin{array}{l}AE=AF\\AD=AD\\DE=DF\end{array}\right.$
∴△AED≌△AFD(SSS)。
∴∠EAD=∠FAD。
即AD平分∠BAC。
5. 如图是高空救援时会用到的升降台,其四边形结构可以任意伸缩,调节高度,它凸显了四边形的 (
A.稳定性
B.不稳定性
C.美观性
D.平衡性
6. 如图是深井救援时常用的救援三脚架,为了使其在救援时更加稳固,会用绳索将三个支撑点连接,其中蕴含的数学原理是______.
B
)A.稳定性
B.不稳定性
C.美观性
D.平衡性
6. 如图是深井救援时常用的救援三脚架,为了使其在救援时更加稳固,会用绳索将三个支撑点连接,其中蕴含的数学原理是______.
答案:
5. B
6. 三角形的稳定性
6. 三角形的稳定性
查看更多完整答案,请扫码查看


