《2025年万唯中考情境题八年级数学上册苏科版》

9. (教材复习题第4题改编)如图,在△ABC和△BCD中,∠ABC= ∠BDC= 90°,AC= 13,BD= 4,CD= 3,则AB的长为 (C)
A.5
B.9
C.12
D.16

答案： C

10. 如图,在△ABC中,AC⊥BC,AD是BC边上的中线,AC= 2, $ AD= \sqrt{7} $,则AB的值为4.

答案： 4

11. 如图是“勾股树”的一部分,图中所有的三角形都是直角三角形,四边形都是正方形,若AB= 6,则图中阴影部分的面积和为36.
12. 如图,在Rt△ABC中,∠C= 90°,在AB同侧分别以AB,AC,BC为直径作三个半圆,若△ABC的面积为5,则图中阴影部分(即“希波克拉底月牙形”)的面积为5.

答案： 11. 36 12. 5

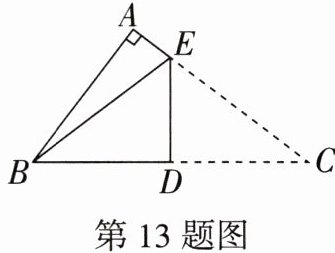
13. 如图,在△ABC中,∠A= 90°,AB= 6,AC= 8,将△ABC沿DE折叠,折叠后点C与点B重合
(1)求BD的长度;
(2)求CE的长度.

答案： 解:
(1)
∵在△ABC中,$\angle A=90^{\circ}$,AB=6,AC=8,
∴根据勾股定理可得$BC^{2}=AB^{2}+AC^{2}=6^{2}+8^{2}=$100,即BC=10.
∵折叠后点C与点B重合,
∴点D是BC的中点,
$\therefore BD=\frac{1}{2}BC=5$;
(2)由折叠可知BE=CE.
在Rt△ABE中,由勾股定理可得$BE^{2}=AB^{2}+AE^{2}$,
∵AE=AC-CE=8-CE,
$\therefore CE^{2}=6^{2}+(8-CE)^{2}$,
解得$CE=\frac{25}{4}$.

1. (逆袭卷改编)如图,将长方形ABCD沿对角线AC折叠,AD的对应边AD'交BC于点E,已知AD= 8,AB= 4,则BE的长为3.

答案： 3

2. 如图,在Rt△ABC中,∠ABC= 90°,AB= 6,BC= 4,点D,F在斜边AC上,点G在边AB上,将△BCD沿BD折叠,点C恰好落在斜边AC上的点E处,折痕为BD,再将△AFG沿FG折叠,点A也落在点E处,折痕为FG,则AG的长为$\frac{5}{3}$.

答案： $\frac{5}{3}$