第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 下列各组数,是勾股数的是 (
A.$0.3$,$0.4$,$0.5$
B.$6$,$8$,$10$
C.$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$
D.$1$,$\sqrt{2}$,$3$
B
)A.$0.3$,$0.4$,$0.5$
B.$6$,$8$,$10$
C.$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$
D.$1$,$\sqrt{2}$,$3$
答案:
B
2. 观察下列几组勾股数的组成特点,并填空:① $3$,$4$,$5$;② $6$,$8$,$10$;③ $9$,$12$,$15$;…,则第⑥组勾股数为______
18,24,30
.
答案:
18,24,30
3. 如下表是古希腊的柏拉图和我国古代数学著作《九章算术》分别给出的勾股数公式:
|柏拉图|如果$m表示大于1$的整数,$a = 2m$,$b = m^{2}-1$,$c = m^{2}+1$,那么$a$,$b$,$c$为勾股数.|
|《九章算术》|$a= \frac{1}{2}(m^{2}-n^{2})$,$b = mn$,$c= \frac{1}{2}(m^{2}+n^{2})$,其中$m>n>0$,$m$,$n$是互质的奇数(注:$a$,$b$,$c$的相同倍数组成的一组数也是勾股数).|
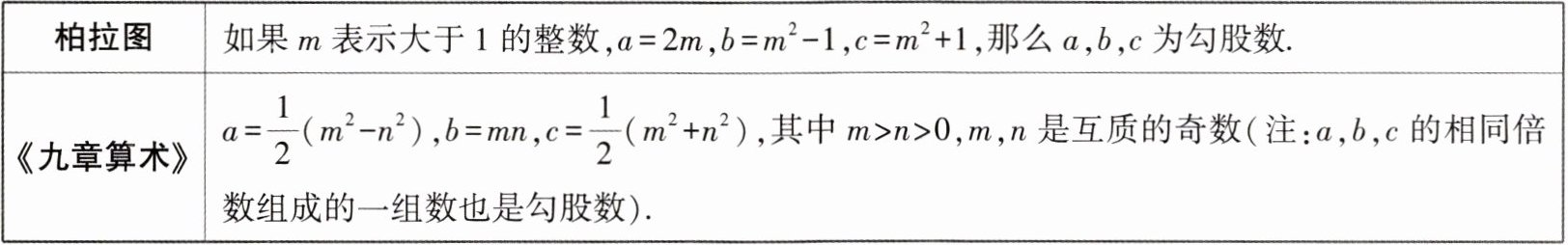
(1)小明查阅资料发现柏拉图公式存在缺陷,试写出一组柏拉图公式无法构造的勾股数:______
(2)根据《九章算术》中的记载,当$m = 5$,$n = 3$时,这组勾股数为______
|柏拉图|如果$m表示大于1$的整数,$a = 2m$,$b = m^{2}-1$,$c = m^{2}+1$,那么$a$,$b$,$c$为勾股数.|
|《九章算术》|$a= \frac{1}{2}(m^{2}-n^{2})$,$b = mn$,$c= \frac{1}{2}(m^{2}+n^{2})$,其中$m>n>0$,$m$,$n$是互质的奇数(注:$a$,$b$,$c$的相同倍数组成的一组数也是勾股数).|
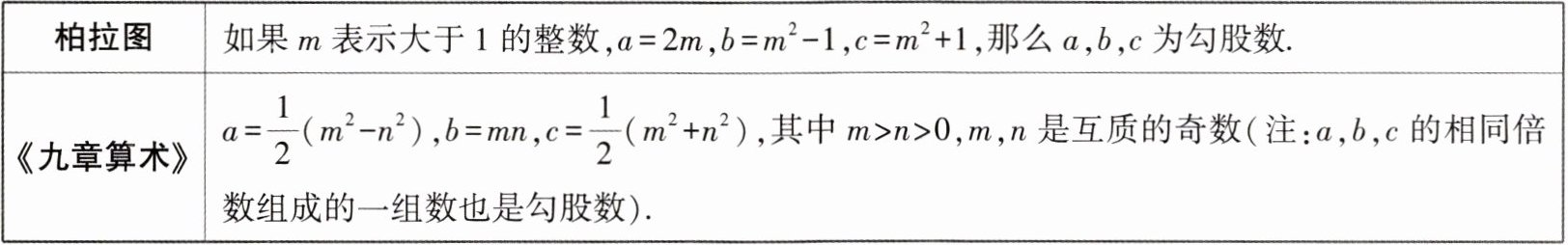
(1)小明查阅资料发现柏拉图公式存在缺陷,试写出一组柏拉图公式无法构造的勾股数:______
5,12,13
;(2)根据《九章算术》中的记载,当$m = 5$,$n = 3$时,这组勾股数为______
8,15,17
.
答案:
解:
(1)5,12,13(答案不唯一);
(2)8,15,17
(1)5,12,13(答案不唯一);
(2)8,15,17
【阅读材料】已知直角三角形的两条直角边长为$a$,$b$,斜边长为$c$,将满足$a^{2}+b^{2}= c^{2}$的一组正整数称为“勾股数组”,记为$(a,b,c)$,其中$a\leqslant b<c$. 事实上,早在公元前十一世纪,中国古代数学家商高就发现了“勾三、股四、弦五”,我们将其简记为$(3,4,5)$. 类似的勾股数组还有很多……,例如:$(5,12,13)$,$(7,24,25)$,$(9,40,41)$,$(11,60,61)$,$(13,84,85)$,…
【探究1】(1)请你根据上述的规律写出下一组勾股数组:$(15,$
(2)如果直角三角形的直角边长$a = 2n + 1$($n$为正整数),那么$b + c=$
【探究2】请判断$a^{2}-4$,$4a$,$a^{2}+4$($a为大于2$的正整数)是否为一组“勾股数”,并说明理由.
解:$a^{2}-4$,$4a$,$a^{2}+4$为一组“勾股数”.理由如下:
∵a为大于2的正整数,
∴$a^{2}-4$,$4a$,$a^{2}+4$都为正整数,
∵$(a^{2}-4)^{2}+(4a)^{2}$$=a^{4}-8a^{2}+16+16a^{2}$$=a^{4}+8a^{2}+16$,$=(a^{2}+4)^{2}$,即$(a^{2}-4)^{2}+(4a)^{2}=(a^{2}+4)^{2}$,
∴当a为大于2的正整数时,$a^{2}-4$,$4a$,$a^{2}+4$是一组勾股数.
【探究1】(1)请你根据上述的规律写出下一组勾股数组:$(15,$
112
,113
);(2)如果直角三角形的直角边长$a = 2n + 1$($n$为正整数),那么$b + c=$
$4n^{2}+4n+1$
(用含$n$的代数式表示);【探究2】请判断$a^{2}-4$,$4a$,$a^{2}+4$($a为大于2$的正整数)是否为一组“勾股数”,并说明理由.
解:$a^{2}-4$,$4a$,$a^{2}+4$为一组“勾股数”.理由如下:
∵a为大于2的正整数,
∴$a^{2}-4$,$4a$,$a^{2}+4$都为正整数,
∵$(a^{2}-4)^{2}+(4a)^{2}$$=a^{4}-8a^{2}+16+16a^{2}$$=a^{4}+8a^{2}+16$,$=(a^{2}+4)^{2}$,即$(a^{2}-4)^{2}+(4a)^{2}=(a^{2}+4)^{2}$,
∴当a为大于2的正整数时,$a^{2}-4$,$4a$,$a^{2}+4$是一组勾股数.
答案:
解:【探究1】
(1)112,113;
(2)$4n^{2}+4n+1$;【探究2】$a^{2}-4$,$4a$,$a^{2}+4$为一组“勾股数”.理由如下:
∵a为大于2的正整数,
∴$a^{2}-4$,$4a$,$a^{2}+4$都为正整数,
∵$(a^{2}-4)^{2}+(4a)^{2}$$=a^{4}-8a^{2}+16+16a^{2}$$=a^{4}+8a^{2}+16$,$=(a^{2}+4)^{2}$,即$(a^{2}-4)^{2}+(4a)^{2}=(a^{2}+4)^{2}$,
∴当a为大于2的正整数时,$a^{2}-4$,$4a$,$a^{2}+4$是一组勾股数.
(1)112,113;
(2)$4n^{2}+4n+1$;【探究2】$a^{2}-4$,$4a$,$a^{2}+4$为一组“勾股数”.理由如下:
∵a为大于2的正整数,
∴$a^{2}-4$,$4a$,$a^{2}+4$都为正整数,
∵$(a^{2}-4)^{2}+(4a)^{2}$$=a^{4}-8a^{2}+16+16a^{2}$$=a^{4}+8a^{2}+16$,$=(a^{2}+4)^{2}$,即$(a^{2}-4)^{2}+(4a)^{2}=(a^{2}+4)^{2}$,
∴当a为大于2的正整数时,$a^{2}-4$,$4a$,$a^{2}+4$是一组勾股数.
查看更多完整答案,请扫码查看


