第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
6. 传统文化情境 琴棋书画 晓晓在如图所示的部分象棋棋盘(四个小正方形边长均相同)中画出了“马”从点A可以行棋的路线AB和AC,则∠1+∠2的度数为 (
A.110°
B.120°
C.150°
D.180°
D
)A.110°
B.120°
C.150°
D.180°
答案:
D
7. 如图,E是∠BAC平分线AD上的一点,若AB= 6,AC= 10,BE= 4,则CE的长可能是 (
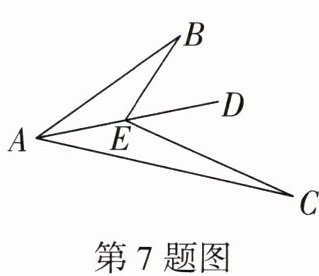
A.7
B.8
C.9
D.10
A
)
A.7
B.8
C.9
D.10
答案:
A
8. 如图,在△ABC中,∠B= ∠C,D,E,F分别是AB,AC,BC上的点,连接DF,EF,且BD= CF,BF= CE. 若∠A= 100°,则∠DFE的度数为______
40°
.
答案:
40°
9. 如图,在△ABC中,AC= 4,AD平分∠BAC交BC于点D,在AB上截取AE= AC,连接DE. 若△BDE的周长为7,则△ABC的周长为
15
.
答案:
15
10. 如图,△ABC和△ADE均为等腰直角三角形,∠BAC= ∠DAE= 90°,点D在BC上,连接EC.
(1)求证:△ABD≌△ACE;
(2)若∠EDC= 55°,求∠DEC的度数.
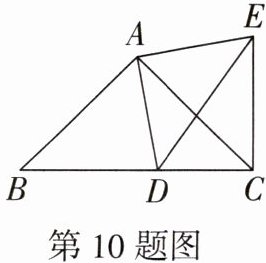
(1)求证:△ABD≌△ACE;
(2)若∠EDC= 55°,求∠DEC的度数.

答案:
(1)证明:
∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,
∴∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE,在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS);
(2)解:由
(1)得,△ABD≌△ACE,∠B=∠ACB=45°,
∴∠ACE=∠B=∠ACB=45°,
∴∠DCE=90°,
∵∠EDC=55°,
∴∠DEC=90° - 55° = 35°.
(1)证明:
∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,
∴∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE,在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS);
(2)解:由
(1)得,△ABD≌△ACE,∠B=∠ACB=45°,
∴∠ACE=∠B=∠ACB=45°,
∴∠DCE=90°,
∵∠EDC=55°,
∴∠DEC=90° - 55° = 35°.
11. (中考新考法·解题方法型阅读理解题)【问题提出】倍长中线法是一种重要的解题方法,如图①,在△ABC中,AD是BC边上的中线,若延长AD至点E,使DE= AD,连接CE,可根据“SAS”证明△ABD≌△ECD,则AB= EC.
【解决问题】如图②,在Rt△ABO和Rt△CDO中,∠AOB= ∠COD= 90°,OA= OB,OC= OD,连接AC,BD,E是BD的中点,连接OE,求证:$OE= \frac {1}{2}AC$.
[此考法江苏、四川等地中考已考查]
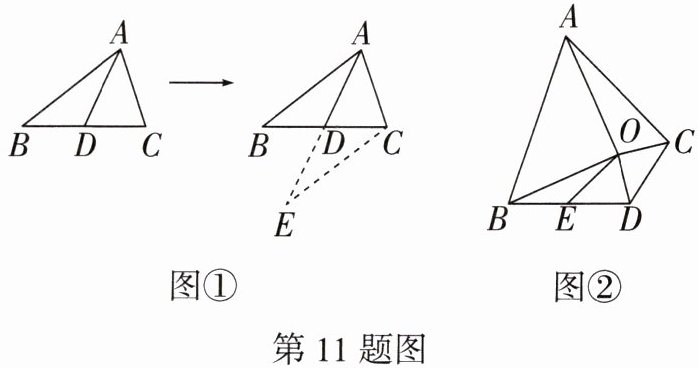
【解决问题】如图②,在Rt△ABO和Rt△CDO中,∠AOB= ∠COD= 90°,OA= OB,OC= OD,连接AC,BD,E是BD的中点,连接OE,求证:$OE= \frac {1}{2}AC$.
[此考法江苏、四川等地中考已考查]

答案:
证明:如解图,延长OE至点F,使得EF=OE,连接BF.
∵E是BD的中点,
∴BE=DE.在△BEF和△DEO中,EF=EO,∠BEF=∠DEO,BE=DE,
∴△BEF≌△DEO(SAS),(关键点:延长已知中线到某点,使新线段的长度等于已知中线的长度,再利用SAS证明两个三角形全等,隐含条件为对顶角相等)
∴BF=OD=OC,∠FBE=∠ODE,
∴BF//OD,
∴∠OBF=∠OBE+∠FBE=180° - ∠BOD,
∵∠AOC=360° - ∠AOB - ∠COD - ∠BOD=180° - ∠BOD,
∴∠OBF=∠AOC,在△OBF和△AOC中,OB=AO,∠OBF=∠AOC,BF=OC,
∴△OBF≌△AOC(SAS),
∴OF=AC,
∵OE= $\frac{1}{2}$OF,
∴OE= $\frac{1}{2}$AC.
∵E是BD的中点,
∴BE=DE.在△BEF和△DEO中,EF=EO,∠BEF=∠DEO,BE=DE,
∴△BEF≌△DEO(SAS),(关键点:延长已知中线到某点,使新线段的长度等于已知中线的长度,再利用SAS证明两个三角形全等,隐含条件为对顶角相等)
∴BF=OD=OC,∠FBE=∠ODE,
∴BF//OD,
∴∠OBF=∠OBE+∠FBE=180° - ∠BOD,
∵∠AOC=360° - ∠AOB - ∠COD - ∠BOD=180° - ∠BOD,
∴∠OBF=∠AOC,在△OBF和△AOC中,OB=AO,∠OBF=∠AOC,BF=OC,
∴△OBF≌△AOC(SAS),
∴OF=AC,
∵OE= $\frac{1}{2}$OF,
∴OE= $\frac{1}{2}$AC.
查看更多完整答案,请扫码查看


