第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. (教材练习第1题改编)如图,在$\triangle ABC$中,点D为BC的中点,点E为AC的中点,则下列说法不正确的是(

A.AD是$\triangle ABC$的中线
B.DE是$\triangle ADC$的中线
C.DE是$\triangle ABC$的中线
D.$BD= CD$,$CE= AE$
C
)
A.AD是$\triangle ABC$的中线
B.DE是$\triangle ADC$的中线
C.DE是$\triangle ABC$的中线
D.$BD= CD$,$CE= AE$
答案:
C
2. (教材练习第3题改编) 一题多变
变式1 利用三角形中线的性质求周长
如图,在$\triangle ABC$中,$AB= 7$,$BC= 9$,BD是AC边上的中线,若$\triangle ABD$的周长为17,则$\triangle BCD$的周长是______.

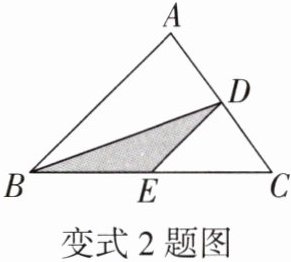
变式2 利用三角形中线的性质求面积
如图,BD是$\triangle ABC$的中线,E是BC边的中点,连接DE,若图中阴影部分的面积为8,则$\triangle DBC$的面积为______,$\triangle ABC$的面积为______.
变式1
变式1 利用三角形中线的性质求周长
如图,在$\triangle ABC$中,$AB= 7$,$BC= 9$,BD是AC边上的中线,若$\triangle ABD$的周长为17,则$\triangle BCD$的周长是______.


变式2 利用三角形中线的性质求面积
如图,BD是$\triangle ABC$的中线,E是BC边的中点,连接DE,若图中阴影部分的面积为8,则$\triangle DBC$的面积为______,$\triangle ABC$的面积为______.
变式1
19
变式2 16
,32
答案:
变式1 19 变式2 16,32
3. (逆袭卷改编)如图,$∠1= ∠2$,$∠3= ∠4$,则下列说法:①AD是$\triangle ABC$的角平分线;②BE是$\triangle ABC$的角平分线;③BE是$\triangle ABD$的角平分线,其中正确的有
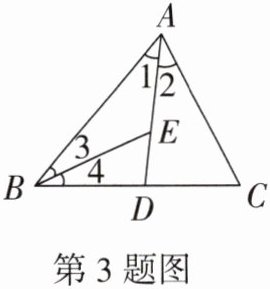
①③
(填序号).
答案:
①③
4. 传统文化情境 苏州折扇 苏州折扇,古称文人扇,怀袖雅物.如图,小敏在折扇的扇骨上连接了A,B两点,与扇钉C构成了$\triangle ABC$,AB分别交中间两根扇骨于D,E两点,已知$∠1= ∠2$,则CD是$\triangle$______
AEC
的角平分线,若CE是$\triangle CDB$的角平分线,$∠ACB= 60^{\circ}$,则$∠3$的度数为______$20^{\circ }$
.
答案:
AEC,$20^{\circ }$
5. (教材习题第8题改编)如图,CD是$\triangle ABC$的角平分线,点E是BC上一点,且$∠EDC= ∠DCE$.求证:$∠BDE= ∠A$.
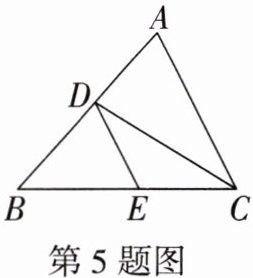

答案:
证明:
∵ CD是$△ABC$的角平分线,
∴$∠DCE=∠ACD$
∵$∠EDC=∠DCE$
∴$∠EDC=∠ACD$
∴$DE// AC$
∴$∠BDE=∠A$
∵ CD是$△ABC$的角平分线,
∴$∠DCE=∠ACD$
∵$∠EDC=∠DCE$
∴$∠EDC=∠ACD$
∴$DE// AC$
∴$∠BDE=∠A$
6. 下列关于$\triangle ABC$的边BC上的高的作法正确的是(

A.
B.
C.
D.
C
) 
A.
B.
C.
D.
答案:
C
7. 三角形的三条高线所在直线的交点在三角形的一个顶点上,则此三角形是(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
答案:
B
8. 如图,在$\triangle ABC$中,线段AD为BC边上的高,点E在线段CD上,连接AE,则AD与BC的位置关系是AD
$\perp$
BC.在$\triangle ABD$中,AD边上的高是线段BD
,在$\triangle AEC$中,CE边上的高是线段AD
.
答案:
$\perp$,BD,AD
9. 如图,在$\triangle ABC$中,BD是AC边上的高,已知$AB= 5$,$AC= 7$,$BD= 2$.
(1)请画出AB边上的高CE;
(2)求CE的长.

(1)请画出AB边上的高CE;
(2)求CE的长.

答案:
解:
(1)画AB边上的高CE如解图所示;

(2)
∵$AC=7,BD=2$
∴$S_{\triangle ABC}=\frac {1}{2}AC\cdot BD=\frac {1}{2}×7×2=7$
又
∵$S_{\triangle ABC}=\frac {1}{2}AB\cdot CE,AB=5$
∴$CE=\frac {2S_{\triangle ABC}}{AB}=\frac {2×7}{5}=\frac {14}{5}$
解:
(1)画AB边上的高CE如解图所示;

(2)
∵$AC=7,BD=2$
∴$S_{\triangle ABC}=\frac {1}{2}AC\cdot BD=\frac {1}{2}×7×2=7$
又
∵$S_{\triangle ABC}=\frac {1}{2}AB\cdot CE,AB=5$
∴$CE=\frac {2S_{\triangle ABC}}{AB}=\frac {2×7}{5}=\frac {14}{5}$
查看更多完整答案,请扫码查看


