《2025年万唯中考情境题八年级数学上册苏科版》

12. 如图,已知点$B$,$F$,$C$在同一条直线上,$AC与DF交于点E$,$AB= CD$,$AC= CF$,$BC= DF$.
(1)求证:$△ABC\cong △CDF$;
(2)若$∠BCA= 20^{\circ}$,求$∠AEF$的度数.

答案： 12.
(1)证明:在△ABC和△CDF中,{AB=CD,AC=CF,BC=DF,
∴△ABC≌△CDF(SSS);
(2)解:由
(1)得,△ABC≌△CDF,
∵∠BCA=20°,
∴∠DFC=∠BCA=20°,
∴∠AEF=∠BCA+∠DFC=40°.

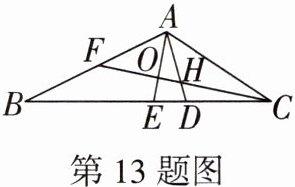
13. 如图,在$△ABC$中,$AD⊥BC于点D$,$AE平分∠BAC交BC于点E$,$CF平分∠ACB交AD于点H$,交$AE于点O$,且$∠AFH= ∠AHF$.
(1)求证:$△ABC$是直角三角形;
(2)若$∠DAC= 26^{\circ}$,求$∠BFC$的度数.

答案： 13.
(1)证明:
∵AD⊥BC,
∴∠CHD+∠HCD=90°,
∵CF平分∠ACB,
∴∠ACF=∠FCD,
∴∠CHD+∠ACF=90°,
又
∵∠AHF=∠CHD,∠AFH=∠AHF,
∴∠AFH+∠ACF=90°,
∴∠BAC=90°,
∴△ABC是直角三角形;
(2)解:由
(1)可知,∠BAC=90°,
∴∠B+∠ACB=90°,
∵AD⊥BC,
∴∠DAC+∠ACD=90°,
∴∠B=∠DAC=26°,∠ACD=90° - 26°=64°,
∵CF平分∠ACB,
∴∠FCB=$\frac{1}{2}$∠ACB=32°,
∴∠BFC=180° - 26° - 32°=122°.

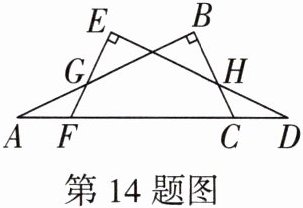
14. 如图,$Rt△ABC与Rt△DEF的顶点A$,$F$,$C$,$D$在同一条直线上,$AB与EF相交于点G$,$BC与DE相交于点H$,$∠B= ∠E= 90^{\circ}$,$AF= CD$,$AB= DE$.
(1)求证:$Rt△ABC\cong Rt△DEF$;
(2)若$GF= 1$,求线段$CH$的长.

答案： 14.
(1)证明:
∵AF=CD,
∴AF+CF=CD+CF,即AC=DF.
在Rt△ABC和Rt△DEF中,{AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL);
(2)解:由
(1)得,Rt△ABC≌Rt△DEF,
∴∠A=∠D,∠EFD=∠BCA.
∵∠AFG=180° - ∠EFD,∠DCH=180° - ∠BCA,
∴∠AFG=∠DCH.
在△AFG和△DCH中,{∠A=∠D,AF=DC,∠AFG=∠DCH,
∴△AFG≌△DCH(ASA),
∴CH=FG=1.

15. 日常生活情境 活动宣传板 育才中学打算举办校园文化艺术节,小西同学负责此次艺术节宣传板的制作任务,如图,将该宣传板垂直于地面放置时,点$A$,$C$,$E到地面的距离分别是60cm$,$20cm$,$80cm$,过点$A作AF⊥BD$,交$DB的延长线于点F$,过点$C作CG⊥BD于点G$.已知$AB= BC且AB⊥BC$,$CD= DE且CD⊥DE$.
(1)求证:$△ABF\cong △BCG$;
(2)请你帮小西同学计算出这块宣传板的面积.

答案： 15.
(1)证明:
∵AF⊥BF,CG⊥BD,
∴∠AFB=∠BGC=90°,
∴∠BAF+∠ABF=90°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABF+∠CBG=90°,
∴∠BAF=∠CBG,
在△ABF和△BCG中,{∠AFB=∠BGC,∠BAF=∠CBG,AB=BC,
∴△ABF≌△BCG(AAS);
(2)解:如解图,过点E作EH⊥BD交BD的延长线于点H.
由题意可知,AF=60cm,CG=20cm,EH=80cm.
由
(1)得,△ABF≌△BCG,
∴AF=BG=60cm,BF=CG=20cm,
同理可证△CDG≌△DEH,
∴DG=EH=80cm,CG=DH=20cm,
∴FH=BF+BG+DG+DH=180cm,
∴S=S梯形AFHE - 2S△ABF - 2S△DEH=$\frac{1}{2}$(AF+EH)·FH - 2×$\frac{1}{2}$AF·BF - 2×$\frac{1}{2}$EH·DH=$\frac{1}{2}$×(60+80)×180 - 2×$\frac{1}{2}$×60×20 - 2×$\frac{1}{2}$×80×20=9800cm²,
∴这块宣传板的面积为9800cm².