第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
8. (教材例3改编)如图,AB//DE,AC//DF,AC= DF,下列条件中不能判断△ABC≌△DEF的是 (
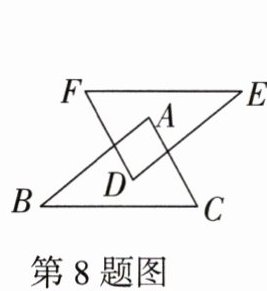
A.AB= DE
B.∠B= ∠E
C.EF= BC
D.EF//BC
C
)
A.AB= DE
B.∠B= ∠E
C.EF= BC
D.EF//BC
答案:
C
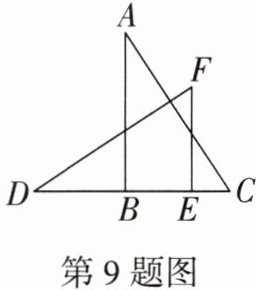
9. Rt△ABC和Rt△DEF按如图方式摆放,D,B,E,C四点在同一直线上,已知AC= DF. AC⊥DF,若AB= 5,CD= 6,EF= 3,则BE的长为______
B
.
答案:
B
10. 跨学科情境 物理单摆实验 如图①,是一个单摆小球实验器,如图②,是小球摆动过程中的示意图. 已知摆线长OA= OB= OC= 90 cm,当摆线位于OB位置时,过点B作BD⊥OA于点D,测得AD= 10 cm,当摆线位于OC位置时,OC⊥OB,则此时小球到OA的水平距离为______
80
cm.
答案:
80
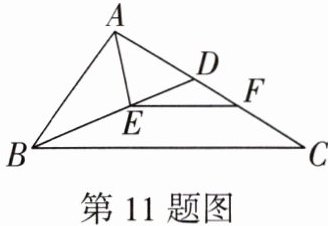
11. 如图,在△ABC中,D是AC边上一点,连接BD,AE平分∠BAC交BD于点E,EF//BC交AC于点F. 已知∠ABE= ∠C.
(1)求证:△ABE≌△AFE;
(2)若BD= 8,AB= 7,AD= 5,求△DEF的周长.
(1)求证:△ABE≌△AFE;
(2)若BD= 8,AB= 7,AD= 5,求△DEF的周长.

答案:
(1)证明:
∵AE 平分∠BAC,
∴∠BAE=∠FAE.
∵EF//BC,
∴∠AFE=∠C.又
∵∠ABE=∠C,
∴∠ABE=∠AFE.在△ABE 和△AFE 中,∠ABE=∠AFE,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE(AAS);
(2)解:由
(1)得:△ABE≌△AFE,
∴AB=AF=7,BE=FE.
∴DE+EF=DE+BE=BD=8.又
∵AD=5.
∴DF=AF - AD=7 - 5=2,
∴△DEF 的周长=DE+EF+DF=BD+DF=10.
(1)证明:
∵AE 平分∠BAC,
∴∠BAE=∠FAE.
∵EF//BC,
∴∠AFE=∠C.又
∵∠ABE=∠C,
∴∠ABE=∠AFE.在△ABE 和△AFE 中,∠ABE=∠AFE,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE(AAS);
(2)解:由
(1)得:△ABE≌△AFE,
∴AB=AF=7,BE=FE.
∴DE+EF=DE+BE=BD=8.又
∵AD=5.
∴DF=AF - AD=7 - 5=2,
∴△DEF 的周长=DE+EF+DF=BD+DF=10.
12. (中考新考法·解题方法型阅读理解题)在学习全等三角形的过程中,我们学会了用“截长补短”法来构造全等三角形,如图①,在四边形ABCD中,∠ABC= ∠ADC= 90°,AD= DC,若BD= 8 cm,求四边形ABCD的面积.
解:延长BC至点E,使得CE= AB,连接DE,可证明△ABD≌△CED(SAS),根据全等三角形的性质得DE= BD= 8 cm,∠BDE= ∠ADC= 90°,得S_{四边形ABCD}= S_{△ABD}+S_{△BDC}= S_{△BDC}+S_{△DEC}= S_{△BDE},那么四边形ABCD的面积就转化成△BDE的面积.
(1)根据上面的思路,我们可以求得四边形ABCD的面积为______cm^{2};
(2)如图②,在五边形ABCDE中,AB= AE= 8 cm,BC= 4 cm,DE= 3 cm,∠B= ∠E= 90°,AC,AD分别平分∠BCD,∠CDE,你是否可以用上面的方法求五边形ABCDE的面积呢?
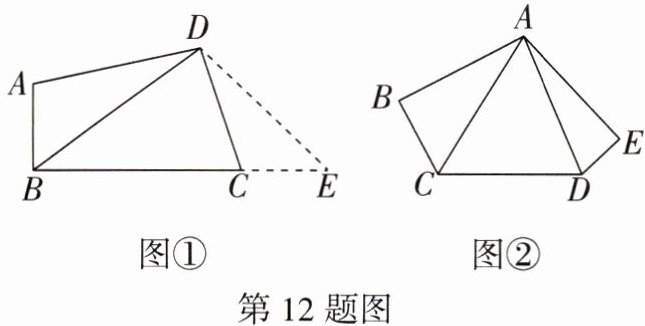
解:延长BC至点E,使得CE= AB,连接DE,可证明△ABD≌△CED(SAS),根据全等三角形的性质得DE= BD= 8 cm,∠BDE= ∠ADC= 90°,得S_{四边形ABCD}= S_{△ABD}+S_{△BDC}= S_{△BDC}+S_{△DEC}= S_{△BDE},那么四边形ABCD的面积就转化成△BDE的面积.
(1)根据上面的思路,我们可以求得四边形ABCD的面积为______cm^{2};
(2)如图②,在五边形ABCDE中,AB= AE= 8 cm,BC= 4 cm,DE= 3 cm,∠B= ∠E= 90°,AC,AD分别平分∠BCD,∠CDE,你是否可以用上面的方法求五边形ABCDE的面积呢?

答案:
解:
(1)32;
(2)可以.如解图,延长 CB 至点 F,使 BF=DE,连接 AF,则∠ABF=∠ABC=90°.在△ABF 和△AED 中,FB=DE,∠ABF=∠AED,AB=AE,
∴△ABF≌△AED(SAS),
∴∠F=∠ADE.
∵AC,AD 分别平分∠BCD,∠CDE,
∴∠ACB=∠ACD,∠ADC=∠ADE,
∴∠F=∠ADC,在△AFC 和△ADC 中,∠F=∠ADC,∠ACF=∠ACD,AC=AC,
∴△AFC≌△ADC(AAS),
∵BC=4 cm,FB=DE=3 cm,
∴FC=7 cm,
∵S△AFC=1/2AB·FC=1/2×8×7=28(cm²),
∴S△ADC=S△AFC=28 cm²,
∴五边形 ABCDE 的面积=S△ADC+S△ABC+S△ADE=S△ADC+S△AFC=56(cm²).
解:
(1)32;
(2)可以.如解图,延长 CB 至点 F,使 BF=DE,连接 AF,则∠ABF=∠ABC=90°.在△ABF 和△AED 中,FB=DE,∠ABF=∠AED,AB=AE,
∴△ABF≌△AED(SAS),
∴∠F=∠ADE.
∵AC,AD 分别平分∠BCD,∠CDE,
∴∠ACB=∠ACD,∠ADC=∠ADE,
∴∠F=∠ADC,在△AFC 和△ADC 中,∠F=∠ADC,∠ACF=∠ACD,AC=AC,
∴△AFC≌△ADC(AAS),
∵BC=4 cm,FB=DE=3 cm,
∴FC=7 cm,
∵S△AFC=1/2AB·FC=1/2×8×7=28(cm²),
∴S△ADC=S△AFC=28 cm²,
∴五边形 ABCDE 的面积=S△ADC+S△ABC+S△ADE=S△ADC+S△AFC=56(cm²).

查看更多完整答案,请扫码查看


