第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 下列选项中,不能判定$\triangle ABC\cong \triangle DEF$的条件是 (
A.$AB = DE$,$AC = DF$,$\angle A = \angle D$
B.$\angle A = \angle D$,$\angle B = \angle E$,$AC = DF$
C.$AB = DE$,$BC = EF$,$\angle A = \angle D$
D.$AB = DE$,$AC = DF$,$BC = EF$
C
)A.$AB = DE$,$AC = DF$,$\angle A = \angle D$
B.$\angle A = \angle D$,$\angle B = \angle E$,$AC = DF$
C.$AB = DE$,$BC = EF$,$\angle A = \angle D$
D.$AB = DE$,$AC = DF$,$BC = EF$
答案:
C
2. (教材例 1 改编)如图,在四边形 ABCD 中,AC 与 BD 相交于点 O,$\triangle AOB\cong \triangle COD$,则图中全等的三角形有 (
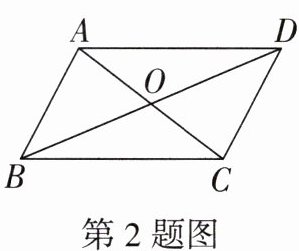
A.1 对
B.2 对
C.3 对
D.4 对
D
)
A.1 对
B.2 对
C.3 对
D.4 对
答案:
D
3. 如图,AD 为$\triangle ABC$的角平分线,点 E 在边 AB 上,$AE = AC$,若$\angle C = 60^{\circ}$,$\angle EDB = 20^{\circ}$,则$\angle B$的度数为 (
A.$40^{\circ}$
B.$35^{\circ}$
C.$30^{\circ}$
D.$25^{\circ}$
A
)A.$40^{\circ}$
B.$35^{\circ}$
C.$30^{\circ}$
D.$25^{\circ}$
答案:
A
4. (中考新考法·选择条件开放)如图,B,E,C 三点共线,已知$AB = AD$,$AD// BC$,$\angle DAB = \angle CAE$,现有下列条件:①$AE = AC$;②$\angle D = \angle DAB$;③$\angle DAC + \angle AED = 180^{\circ}$.选择其中一个作为条件来证明:$\triangle DAE\cong \triangle BAC$.
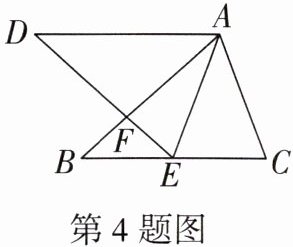

答案:
解:选择条件①,证明如下:
∵∠DAB=∠CAE,
∴∠DAB+∠EAB=∠CAE+∠EAB,即∠DAE=∠BAC.
在△DAE和△BAC中,{AE=AC,∠DAE=∠BAC,AD=AB}
∴△DAE≌△BAC(SAS).
选择条件②、条件③见详解.
(选择一个条件证明即可)
∵∠DAB=∠CAE,
∴∠DAB+∠EAB=∠CAE+∠EAB,即∠DAE=∠BAC.
在△DAE和△BAC中,{AE=AC,∠DAE=∠BAC,AD=AB}
∴△DAE≌△BAC(SAS).
选择条件②、条件③见详解.
(选择一个条件证明即可)
5. (教材复习题第 13 题改编)如图,已知$BF\perp AC$,$CE\perp AB$,CE 交 BF 于点 D,AD 平分$\angle BAC$.
(1)求证:$\triangle AFD\cong \triangle AED$;
(2)一题多解法 求证:$AB = AC$.

(1)求证:$\triangle AFD\cong \triangle AED$;
(2)一题多解法 求证:$AB = AC$.

答案:
证明:
(1)
∵BF⊥AC,CE⊥AB,
∴∠AFD=∠AED=90°,
∵AD平分∠BAC,
∴∠FAD=∠EAD,
在△AFD和△AED中,{∠AFD=∠AED,∠FAD=∠EAD,AD=AD}
∴△AFD≌△AED(AAS);
(2)由
(1)得,△AFD≌△AED,
∴AF=AE,
在△BAF和△CAE中,{∠FAB=∠EAC,AF=AE,∠AFB=∠AEC}
∴△BAF≌△CAE(ASA),
∴AB=AC.
证法二:见详解
(1)
∵BF⊥AC,CE⊥AB,
∴∠AFD=∠AED=90°,
∵AD平分∠BAC,
∴∠FAD=∠EAD,
在△AFD和△AED中,{∠AFD=∠AED,∠FAD=∠EAD,AD=AD}
∴△AFD≌△AED(AAS);
(2)由
(1)得,△AFD≌△AED,
∴AF=AE,
在△BAF和△CAE中,{∠FAB=∠EAC,AF=AE,∠AFB=∠AEC}
∴△BAF≌△CAE(ASA),
∴AB=AC.
证法二:见详解
6. 跨学科情境 物理小孔成像 如图①是“小孔成像”的实验图片,图②是其简化示意图. 点 O 代表小孔,AB 代表蜡烛的火苗,CD 代表火苗在光屏上所成的像,$AB// CD$.已知当小孔到蜡烛的距离(物距)等于小孔到光屏的距离(像距)时,所成像的大小与火苗大小相等,请你用数学知识解释这种现象.
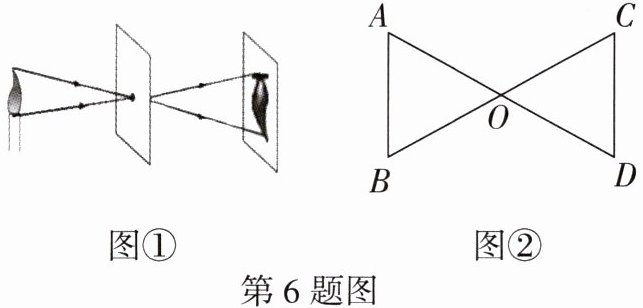

答案:
解:如解图,过点O作EF⊥AB于点E,交CD于点F,则OE代表物距,OF代表像距.
根据题意得AB//CD,OE=OF,
∴∠AEO=∠BEO=∠CFO=∠DFO=90°.
在△AEO和△DFO中,{∠AEO=∠DFO,EO=FO,∠AOE=∠DOF}
∴△AEO≌△DFO(ASA).
∴AE=DF.
同理可证△BEO≌△CFO(ASA),
∴BE=CF.
∴AE+BE=DF+CF,即AB=CD.
∴当物距等于像距时,所成像的大小与火苗大小相等

解:如解图,过点O作EF⊥AB于点E,交CD于点F,则OE代表物距,OF代表像距.
根据题意得AB//CD,OE=OF,
∴∠AEO=∠BEO=∠CFO=∠DFO=90°.
在△AEO和△DFO中,{∠AEO=∠DFO,EO=FO,∠AOE=∠DOF}
∴△AEO≌△DFO(ASA).
∴AE=DF.
同理可证△BEO≌△CFO(ASA),
∴BE=CF.
∴AE+BE=DF+CF,即AB=CD.
∴当物距等于像距时,所成像的大小与火苗大小相等

查看更多完整答案,请扫码查看


