第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
9. 如图,在△ABC中,AB= AC,点A在线段MN上,连接MB,NC并延长,交于点P,已知∠BAM= ∠ACN= 90°,AN= BM. 若∠P= 60°,则∠BAC的度数为(
A.30°
B.45°
C.50°
D.60°
D
)A.30°
B.45°
C.50°
D.60°
答案:
D
10. (教材习题第1题改编) 一题多变
变式1 结合平行线求线段长
如图,m//n,点A,B在直线m上,点D,E在直线n上,AD⊥n,点C在AD上,AB+DE= 9,AB= CD,BC= CE,则AD= ______


变式2 改为结合动点判定全等
如图,P,Q分别为射线OM,ON上的动点,∠OCB= ∠QOP= 90°,已知PQ= OB,CB= 6,OC= 12,当OP的长度为______
变式1 结合平行线求线段长
如图,m//n,点A,B在直线m上,点D,E在直线n上,AD⊥n,点C在AD上,AB+DE= 9,AB= CD,BC= CE,则AD= ______
9
.

变式2 改为结合动点判定全等
如图,P,Q分别为射线OM,ON上的动点,∠OCB= ∠QOP= 90°,已知PQ= OB,CB= 6,OC= 12,当OP的长度为______
6或12
时,△OBC与△QPO全等.
答案:
变式1 9 变式2 6或12
11. 如图,在四边形ABCD中,∠AEB= ∠D= 90°,AB= AF,BE= DF.
(1)求证:Rt△ABE≌Rt△AFD;
(2)若BC= 17,DF= 6,求CF的长.
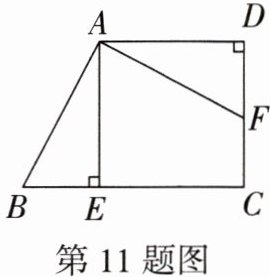
(1)求证:Rt△ABE≌Rt△AFD;
(2)若BC= 17,DF= 6,求CF的长.

答案:
(1)证明:
∵∠AEB=∠D=90°,
在Rt△ABE和Rt△AFD中,{AB=AF,BE=DF}
∴Rt△ABE≌Rt△AFD(HL);
(2)解:如解图,连接AC.
∵Rt△ABE≌Rt△AFD,
∴AE=AD.
在Rt△AEC和Rt△ADC中,{AC=AC,AE=AD}
∴Rt△AEC≌Rt△ADC(HL),
∴CE=CD.
∵BC=17,DF=6,
∴BE=6,
∴CE=CD=17−6=11,
∴CF=CD−DF=11−6=5.
(1)证明:
∵∠AEB=∠D=90°,
在Rt△ABE和Rt△AFD中,{AB=AF,BE=DF}
∴Rt△ABE≌Rt△AFD(HL);
(2)解:如解图,连接AC.
∵Rt△ABE≌Rt△AFD,
∴AE=AD.
在Rt△AEC和Rt△ADC中,{AC=AC,AE=AD}
∴Rt△AEC≌Rt△ADC(HL),
∴CE=CD.
∵BC=17,DF=6,
∴BE=6,
∴CE=CD=17−6=11,
∴CF=CD−DF=11−6=5.
12. (中考新考法·补充证明过程)如图①,已知在△ABC和△DEF中,AB= DE,AC= DF,∠B= ∠E. 在此条件下,对它“强化条件”,分别得到下列三个命题.
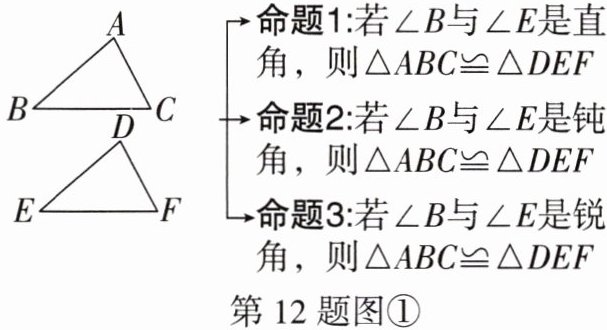
(1)命题1是否为真命题,请说明理由;
(2)命题2是真命题,请将它的证明过程补充完整;
证明:如图②,过点A作AG⊥BC交CB的延长线于点G,过点D作DH⊥EF交FE的延长线于点H,
∴∠AGB= ∠DHE= 90°,
∵∠ABC= ∠DEF,
∴∠ABG= ∠DEH.
在△ABG和△DEH中,…

(3)命题3是假命题,请画出反例并说明理由.

(1)命题1是否为真命题,请说明理由;
(2)命题2是真命题,请将它的证明过程补充完整;
证明:如图②,过点A作AG⊥BC交CB的延长线于点G,过点D作DH⊥EF交FE的延长线于点H,
∴∠AGB= ∠DHE= 90°,
∵∠ABC= ∠DEF,
∴∠ABG= ∠DEH.
在△ABG和△DEH中,…

(3)命题3是假命题,请画出反例并说明理由.
答案:
(1)命题1是真命题.理由如下:
在Rt△ABC和Rt△DEF中,{AB=DE,AC=DF}
∴Rt△ABC≌Rt△DEF(HL),
∴命题1是真命题;
(2)补充证明过程如下:
{∠AGB=∠DHE,∠ABG=∠DEH,AB=DE}
∴△ABG≌△DEH(AAS),
∴AG=DH,
在Rt△ACG和Rt△DFH中,{AG=DH,AC=DF}
∴Rt△ACG≌Rt△DFH(HL),
∴∠C=∠F,
在△ABC和△DEF中,{∠C=∠F,∠ABC=∠DEF,AB=DE}
∴△ABC≌△DEF(AAS);
(3)画图如解图(画法不唯一).
(1)命题1是真命题.理由如下:
在Rt△ABC和Rt△DEF中,{AB=DE,AC=DF}
∴Rt△ABC≌Rt△DEF(HL),
∴命题1是真命题;
(2)补充证明过程如下:
{∠AGB=∠DHE,∠ABG=∠DEH,AB=DE}
∴△ABG≌△DEH(AAS),
∴AG=DH,
在Rt△ACG和Rt△DFH中,{AG=DH,AC=DF}
∴Rt△ACG≌Rt△DFH(HL),
∴∠C=∠F,
在△ABC和△DEF中,{∠C=∠F,∠ABC=∠DEF,AB=DE}
∴△ABC≌△DEF(AAS);
(3)画图如解图(画法不唯一).
查看更多完整答案,请扫码查看


