第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
10. 下列关系式:①$y = 4x$;②$y = 5x - 1$;③$y^{2}= x + 3$;④$|y| = 2x$,其中$y不是x$的函数的个数是(
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:
B
11. 小明发现家里开灯的数量越多,开灯时间越长,用电量越大,电费也会越多.在下列各量中:①开灯的时长;②开灯的数量;③每盏灯平均每小时的耗电量;④每度电的费用;⑤电卡中的剩余费用,其中变量为
①②⑤
,常量为③④
(填序号).
答案:
①②⑤;③④
12. 一只乌鸦在寻找水源的过程中匀速飞行,其速度是$40km/h$,飞行路程为$s(km)$,飞行时间为$t(h)$,用含$t的式子表示s$为
13. 如图,乌鸦找到了一个装有小半瓶水的圆柱形玻璃瓶,由于瓶口狭窄水较浅,它将旁边的石子投入玻璃瓶中使水面上升(假设石子的大小相同),如果瓶中原有水的高度为$10cm$,乌鸦投入10颗石子后,水面上升了$5cm$.
(1)上述过程中哪些是变量,哪些是常量?
(2)当乌鸦投入22颗石子时,水面的高度为多少(水未到达瓶颈口)?
13. 解:
(1)乌鸦给圆柱形玻璃瓶内投放石子的这一过程中,瓶内水的体积未发生变化,水面的高度随投放石子数量的变化而变化,
∴ 水面高度和投放石子数量为变量,水的体积为常量;
(2)
∵ 投入10颗石子的时候,水面上升了5 cm,
∴ 乌鸦每投入一颗石子水面上升$\frac{5}{10}$=0.5(cm),
∴ 乌鸦投入22颗石子时,玻璃瓶中水面上升的高度为22×0.5=11(cm),此时玻璃瓶中水面的高度为11+10=21(cm),故当乌鸦投入22颗石子时,玻璃瓶中水面的高度为21 cm.
s=40t
,这个过程中变量是s和t
,常量是飞行速度40 km/h
.13. 如图,乌鸦找到了一个装有小半瓶水的圆柱形玻璃瓶,由于瓶口狭窄水较浅,它将旁边的石子投入玻璃瓶中使水面上升(假设石子的大小相同),如果瓶中原有水的高度为$10cm$,乌鸦投入10颗石子后,水面上升了$5cm$.
(1)上述过程中哪些是变量,哪些是常量?
(2)当乌鸦投入22颗石子时,水面的高度为多少(水未到达瓶颈口)?

13. 解:
(1)乌鸦给圆柱形玻璃瓶内投放石子的这一过程中,瓶内水的体积未发生变化,水面的高度随投放石子数量的变化而变化,
∴ 水面高度和投放石子数量为变量,水的体积为常量;
(2)
∵ 投入10颗石子的时候,水面上升了5 cm,
∴ 乌鸦每投入一颗石子水面上升$\frac{5}{10}$=0.5(cm),
∴ 乌鸦投入22颗石子时,玻璃瓶中水面上升的高度为22×0.5=11(cm),此时玻璃瓶中水面的高度为11+10=21(cm),故当乌鸦投入22颗石子时,玻璃瓶中水面的高度为21 cm.
答案:
12. s=40t;s和t;飞行速度40 km/h
13. 解:
(1)乌鸦给圆柱形玻璃瓶内投放石子的这一过程中,瓶内水的体积未发生变化,水面的高度随投放石子数量的变化而变化,
∴ 水面高度和投放石子数量为变量,水的体积为常量;
(2)
∵ 投入10颗石子的时候,水面上升了5 cm,
∴ 乌鸦每投入一颗石子水面上升$\frac{5}{10}$=0.5(cm),
∴ 乌鸦投入22颗石子时,玻璃瓶中水面上升的高度为22×0.5=11(cm),此时玻璃瓶中水面的高度为11+10=21(cm),故当乌鸦投入22颗石子时,玻璃瓶中水面的高度为21 cm.
13. 解:
(1)乌鸦给圆柱形玻璃瓶内投放石子的这一过程中,瓶内水的体积未发生变化,水面的高度随投放石子数量的变化而变化,
∴ 水面高度和投放石子数量为变量,水的体积为常量;
(2)
∵ 投入10颗石子的时候,水面上升了5 cm,
∴ 乌鸦每投入一颗石子水面上升$\frac{5}{10}$=0.5(cm),
∴ 乌鸦投入22颗石子时,玻璃瓶中水面上升的高度为22×0.5=11(cm),此时玻璃瓶中水面的高度为11+10=21(cm),故当乌鸦投入22颗石子时,玻璃瓶中水面的高度为21 cm.
14. (教材交流改编)如图,小羽的父亲打算用长15米的篱笆靠墙(足够长)围一块长方形菜地,设菜地的长为$x$米,宽为$y$米.
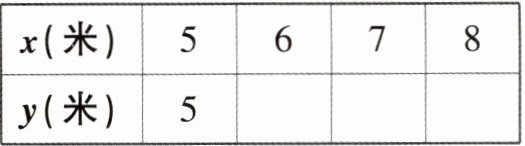
(1)将表格补充完整;
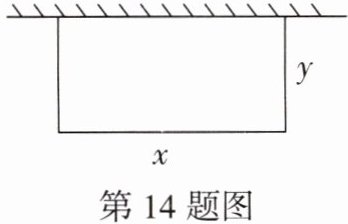
(1)补全表格如下;
x(米) 5 6 7 8
y(米) 5 4.5 4 3.5
(2)y是x的函数.理由如下:
∵ 对于x的每一个值,y都有唯一确定的值与之对应,
∴ y是x的函数.

(1)将表格补充完整;

(1)补全表格如下;
x(米) 5 6 7 8
y(米) 5 4.5 4 3.5
(2)y是x的函数.理由如下:
∵ 对于x的每一个值,y都有唯一确定的值与之对应,
∴ y是x的函数.
答案:
解:
(1)补全表格如下;
x(米) 5 6 7 8
y(米) 5 4.5 4 3.5
(2)y是x的函数.理由如下:
∵ 对于x的每一个值,y都有唯一确定的值与之对应,
∴ y是x的函数.
(1)补全表格如下;
x(米) 5 6 7 8
y(米) 5 4.5 4 3.5
(2)y是x的函数.理由如下:
∵ 对于x的每一个值,y都有唯一确定的值与之对应,
∴ y是x的函数.
15. 如图是由边长相等的等边三角形和正方形组合而成的图形,按照此规律摆下去.
(1)第7个图形中三角形的个数为
(2)设第$n个图形中的三角形的数量为y$个,正方形的数量为$x$个,按上述规律推断$x与y$之间的关系.
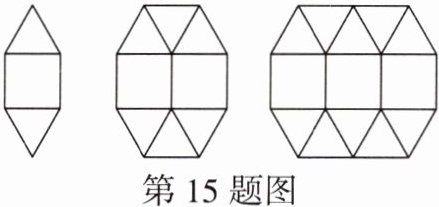
(1)第7个图形中三角形的个数为
26
,正方形的个数为7
;(2)设第$n个图形中的三角形的数量为y$个,正方形的数量为$x$个,按上述规律推断$x与y$之间的关系.

解:∵ 第1个图形正方形的数量为1,三角形的数量为4×1-2=2;第2个图形正方形的数量为2,三角形的数量为4×2-2=6;第3个图形正方形的数量为3,三角形的数量为4×3-2=10,∴ 第n个图形中x与y之间的关系可以用式子表示为y=4x-2.
答案:
解:
(1)26;7;
(2)
∵ 第1个图形正方形的数量为1,三角形的数量为4×1-2=2;第2个图形正方形的数量为2,三角形的数量为4×2-2=6;第3个图形正方形的数量为3,三角形的数量为4×3-2=10,
∴ 第n个图形中x与y之间的关系可以用式子表示为y=4x-2.
(1)26;7;
(2)
∵ 第1个图形正方形的数量为1,三角形的数量为4×1-2=2;第2个图形正方形的数量为2,三角形的数量为4×2-2=6;第3个图形正方形的数量为3,三角形的数量为4×3-2=10,
∴ 第n个图形中x与y之间的关系可以用式子表示为y=4x-2.
查看更多完整答案,请扫码查看


